 por Joana Gabriela » Seg Ago 09, 2010 10:15
por Joana Gabriela » Seg Ago 09, 2010 10:15
A direção de uma escola decidiu enfeitar o pátio com bandeiras coloridas. As bandeiras foram colocadas em
linha reta, na seguinte ordem: 1 bandeira vermelha, 1 azul, 2 vermelhas, 2 azuis, 3 vermelhas, 3 azuis, e
assim por diante.
Depois de colocadas exatamente 99 bandeiras, o número das de cor azul era:
A) 55
B) 60
C) 50
D) 45
-
Joana Gabriela
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Jul 28, 2010 10:13
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Agroecologia
- Andamento: cursando
 por Joana Gabriela » Qua Ago 11, 2010 11:27
por Joana Gabriela » Qua Ago 11, 2010 11:27
Tem resposta não é?
-
Joana Gabriela
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Jul 28, 2010 10:13
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Agroecologia
- Andamento: cursando
 por Douglasm » Qua Ago 11, 2010 20:00
por Douglasm » Qua Ago 11, 2010 20:00
Olá Joana. Pensemos primeiro no seguinte, estamos sempre somando 1 + 1 + 2 + 2 + 3 + 3 + ... ; ou seja estamos somando 2(1 + 2 + 3 + 4 + ... ). Sendo assim, é interessante procurarmos uma soma de números naturais que nos aproxime mais de 99. Sabemos que essa soma é dada por:
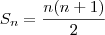
Lembrando que estamos somando dobrado, temos:
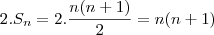
Após poucas tentativas, chegamos a n como sendo no máximo 9 (para n maior que 9, note que teremos 110 bandeiras, o que ultrapassaria o limite de 99). Esclarecendo um pouco mais, queremos descobrir quantas bandeiras foram postas, após a última soma "pareada" (que no caso é 9 vermelhas mais 9 azuis). Continuando:
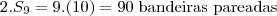
Obviamente, se seguirmos a sequência, deveremos somar mais 10 vermelhas, 10 azuis, etc. Como só temos 99, as últimas a serem somadas foram 9 vermelhas. Finalizando, vemos que o total de bandeiras azuis é metade das 90 bandeiras pareadas, ou seja, é de 45 (alternativa d).
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema sobre bandeiras também.(duvida)
 por ibatexano » Dom Set 13, 2009 02:07
por ibatexano » Dom Set 13, 2009 02:07
- 2 Respostas
- 7542 Exibições
- Última mensagem por ibatexano

Dom Set 13, 2009 15:50
Estatística
-
- Bandeiras
por Rafael16 » Qua Jan 30, 2013 19:23
- 1 Respostas
- 1247 Exibições
- Última mensagem por young_jedi

Qua Jan 30, 2013 22:02
Probabilidade
-
- [Análise Combinatória]Cores das bandeiras.
por francisbarbosa » Seg Fev 27, 2012 20:25
- 1 Respostas
- 1678 Exibições
- Última mensagem por MarceloFantini

Ter Fev 28, 2012 09:49
Estatística
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10715 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
-
- Problema
por Lima » Dom Dez 14, 2008 18:08
- 3 Respostas
- 9727 Exibições
- Última mensagem por blangis

Dom Dez 14, 2008 20:15
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


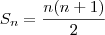
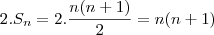
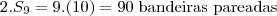



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.