Amigos X e Y? Hahah. Achei engraçado. Enfim...
Vamos usar a variável

como o
instante de tempo em que,convenientemente, o amigo X se encontra na posição

e o amigo Y na posição

.
lara_nsantos escreveu:Sabe-se que Y corre a uma velocidade constante, percorrendo 2,5 metros a cada segundo.
Sem dificuldades podemos escrever
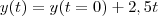
onde

é a posição do amigo Y no intante que começamos a contar o tempo(

).
lara_nsantos escreveu:Para alcançá–lo rapidamente, X usa a estratégia de percorrer 2 metros no 1º segundo; 2,1 metros no 2°segundo; 2,2 metros no 3°segundo, e assim, sucessivamente, aumentando 0,1 metro a cada segundo.
É fácil, novamente, perceber que este movimento é o uniformemente acelerado. Também, pelo título deste tópico, podemos tomar
os deslocamentos 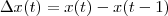
como uma progressão aritmética de razão

com a qual, para calcular o deslocamento total
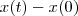
do amigo X, devemos

todos os deslocamentos sucessivos. Faz sentido, não?
Pois bem, sabendo que se trata de uma P.A., os deslocamentos
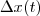
devem obedecer a seguinte expressão:
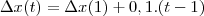
( A famosa

, ok?)
Agora, a
soma destes deslocamentos nos dará a
posição 
do amigo X no instante

. Lembrando que
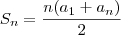
então para o nosso problema escrevemos

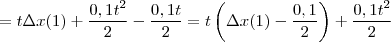
e esta é a ( se você lembrar das aulas da Física) equação do movimento uniformemente acelerado. Para nos convencermos de qe a expressão deve estar certa note que o amigo X, segundo nossa expressão, parte de
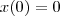
(façamos assim para simplificar as contas) com velocidade inicial diferente de zero. Isto, é, ele estará correndo, como se esperava! Ainda, para

temos
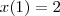
como desejado.
lara_nsantos escreveu:de um mesmo ponto, mas, quando X começa a correr, Y já percorreu 121 metros.

Isto nos diz que devemos tomar
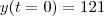
, pois tomamos
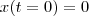
.
Assim, temos as duas equações de movimento e para calcular qual o tempo de encontro basta calcular para qual valor de

que
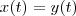
. Faz sentido, não? Se vão se encontrar devem , necessariamente, ocupar a mesma posição!
Resolvendo:
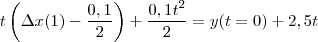
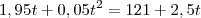
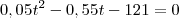
Esta equação de 2° grau tem soluções reais distintas. Isso significa que o ponto de encontro existe e não é único: existem dois instantes que ocorre o encontro dos amigos. As soluções são

ou

. Porém, como estamos interessados em acontecimentos futuros, isto é, soluções com

, nos resta crer que os amigos se encontrarão em

segundos(medimos a distância em metros e a velocidade em m/s)!
É fácil verificar que a posição de encontro será

metros substituindo

em qualquer das duas equações de movimento.
ok? (;


 como o
como o  e o amigo Y na posição
e o amigo Y na posição  .
.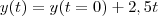 onde
onde  é a posição do amigo Y no intante que começamos a contar o tempo(
é a posição do amigo Y no intante que começamos a contar o tempo( ).
).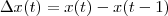 como uma progressão aritmética de razão
como uma progressão aritmética de razão  com a qual, para calcular o deslocamento total
com a qual, para calcular o deslocamento total 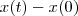 do amigo X, devemos
do amigo X, devemos  todos os deslocamentos sucessivos. Faz sentido, não?
todos os deslocamentos sucessivos. Faz sentido, não?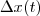 devem obedecer a seguinte expressão:
devem obedecer a seguinte expressão: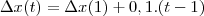
 , ok?)
, ok?)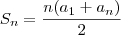 então para o nosso problema escrevemos
então para o nosso problema escrevemos
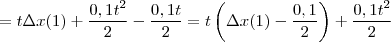
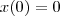 (façamos assim para simplificar as contas) com velocidade inicial diferente de zero. Isto, é, ele estará correndo, como se esperava! Ainda, para
(façamos assim para simplificar as contas) com velocidade inicial diferente de zero. Isto, é, ele estará correndo, como se esperava! Ainda, para  temos
temos 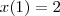 como desejado.
como desejado.
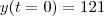 , pois tomamos
, pois tomamos 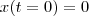 .
.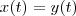 . Faz sentido, não? Se vão se encontrar devem , necessariamente, ocupar a mesma posição!
. Faz sentido, não? Se vão se encontrar devem , necessariamente, ocupar a mesma posição!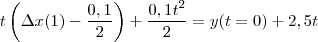
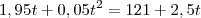
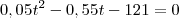
 ou
ou  . Porém, como estamos interessados em acontecimentos futuros, isto é, soluções com
. Porém, como estamos interessados em acontecimentos futuros, isto é, soluções com  , nos resta crer que os amigos se encontrarão em
, nos resta crer que os amigos se encontrarão em  metros substituindo
metros substituindo 


 .
.
 :
: