 por sergioh » Qui Nov 07, 2013 20:07
por sergioh » Qui Nov 07, 2013 20:07
Salve galera,
To com uma dúvida que não to conseguindo resolver, sei lá o que falta...
Olha esse exercicio:
A sucessão (1,a,b,27,c) é uma PG. Calcule a, b e c.
simplismente, não sei!
abraço a todos!
-
sergioh
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Seg Abr 01, 2013 18:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Qui Nov 07, 2013 21:39
por e8group » Qui Nov 07, 2013 21:39
Lembre-se
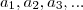
é uma sequência geométrica de razão

se
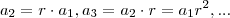
e assim por diante . Por exemplo , as raízes

do polinômio
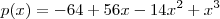
é uma sequência geométrica de razão 2 . Pois podemos escrever ,

como

e
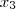
como
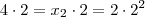
.
Agora tente concluir e comente as dúvidas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por sergioh » Sex Nov 08, 2013 19:57
por sergioh » Sex Nov 08, 2013 19:57
santhiago escreveu:Lembre-se
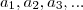
é uma sequência geométrica de razão

se
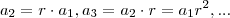
e assim por diante . Por exemplo , as raízes

do polinômio
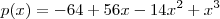
é uma sequência geométrica de razão 2 . Pois podemos escrever ,

como

e
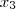
como
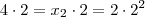
.
Agora tente concluir e comente as dúvidas .
Obrigado santhiago, mas não consegui concluir.
tentei de tudo mas não deu as prespostas: a=3, b=9 e c=81
-
sergioh
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Seg Abr 01, 2013 18:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Sex Nov 08, 2013 20:49
por e8group » Sex Nov 08, 2013 20:49
Considere

. A sucessão
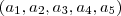
é uma P.G . então existe um número real

constante tal que
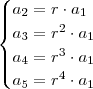
. Só que
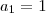
,assim encontrando

determinaremos

. E como sabemos que
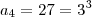
,temos que pelo resultado acima
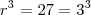
e portanto

. Agora tente concluir.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por sergioh » Dom Nov 10, 2013 15:13
por sergioh » Dom Nov 10, 2013 15:13
Agora entendi sua explicação! Ficou fácil!!! Vlw pela ajuda!
Daqui a poco vai ter mais dúvidas!
Vlw!
-
sergioh
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Seg Abr 01, 2013 18:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



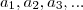 é uma sequência geométrica de razão
é uma sequência geométrica de razão  se
se 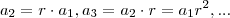 e assim por diante . Por exemplo , as raízes
e assim por diante . Por exemplo , as raízes  do polinômio
do polinômio 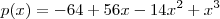 é uma sequência geométrica de razão 2 . Pois podemos escrever ,
é uma sequência geométrica de razão 2 . Pois podemos escrever ,  como
como  e
e 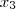 como
como 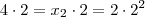 .
.
é uma sequência geométrica de razão
se
e assim por diante . Por exemplo , as raízes
do polinômio
é uma sequência geométrica de razão 2 . Pois podemos escrever ,
como
e
como
.

 . A sucessão
. A sucessão 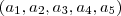 é uma P.G . então existe um número real
é uma P.G . então existe um número real  constante tal que
constante tal que 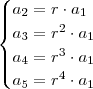 . Só que
. Só que 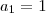 ,assim encontrando
,assim encontrando  determinaremos
determinaremos  . E como sabemos que
. E como sabemos que 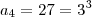 ,temos que pelo resultado acima
,temos que pelo resultado acima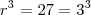 e portanto
e portanto  . Agora tente concluir.
. Agora tente concluir.