 por Leocondeuba » Ter Nov 05, 2013 22:03
por Leocondeuba » Ter Nov 05, 2013 22:03
Desculpem-me pelo meu erro, pois eu não sabia da regra sobre as imagens. Por isso, estou postando novamente a questão.
Olá a todos. Por favor, necessito da resolução desta questão, pois eu tentei resolvê-la e não consegui encontrar o raciocínio certo para me conduzir à alternativa correta. Agradeço desde já.
Sabendo-se que (x1, x2, x3) é uma progressão aritmética de razão 2 e que f:R ? R é uma função quadrática, tal que f(x1) = -2, f(x2) = =14 e f(x3) = -34, é correto afirmar que o coeficiente do termo de 2º grau da função f é igual a
01) 2 02) 1 03) 0,5 04) -1 05) -2
-
Leocondeuba
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Mai 11, 2013 19:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Ter Nov 05, 2013 23:36
por e8group » Ter Nov 05, 2013 23:36
Dica :
Qual relação entre
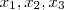
? Por hipótese
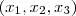
é uma progressão aritmética de razão 2 , então
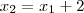
e
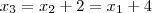
.
Lembre-se
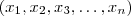
é uma é uma progressão aritmética de razão

, então :
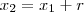
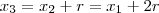
(...)
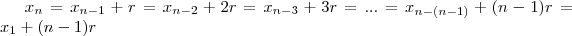
.
Se por hipótese

é uma função quadrática cuja imagem de

por
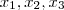
são respct.
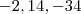
, então suponha que
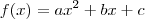
(onde ab,c são constantes a ser determinadas ) .
Agora basta resolver o sistema de equações :
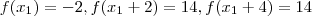
.
Ou se preferir (como eu faria ) , determine
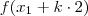
. Obterá algo do gênero
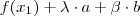
(OBS.: Não fiz a conta apenas verifiquei mentalmente o formato da expressão geral )
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Reta e Circunferência] UESB 2011.2
por Leocondeuba » Ter Nov 05, 2013 22:05
- 0 Respostas
- 1056 Exibições
- Última mensagem por Leocondeuba

Ter Nov 05, 2013 22:05
Geometria Analítica
-
- [Plano Argand-Gauss] UESB 2011.2
por Leocondeuba » Ter Nov 05, 2013 22:06
- 0 Respostas
- 1733 Exibições
- Última mensagem por Leocondeuba

Ter Nov 05, 2013 22:06
Números Complexos
-
- [Geometria Espacial Polinômios] UESB 2011.2
por Leocondeuba » Ter Nov 05, 2013 22:08
- 1 Respostas
- 4199 Exibições
- Última mensagem por DanielFerreira

Dom Jan 31, 2016 21:33
Geometria Espacial
-
- (UNIFOR) Progressão Aritmética e Progressão Harmônica
por andersontricordiano » Ter Mar 22, 2011 12:56
- 1 Respostas
- 6132 Exibições
- Última mensagem por LuizAquino

Ter Mar 22, 2011 13:52
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4724 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


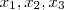 ? Por hipótese
? Por hipótese 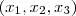 é uma progressão aritmética de razão 2 , então
é uma progressão aritmética de razão 2 , então 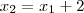 e
e 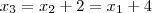 .
. 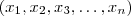 é uma é uma progressão aritmética de razão
é uma é uma progressão aritmética de razão  , então :
, então : 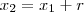
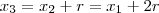
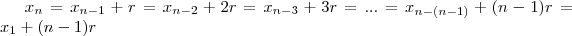 .
. é uma função quadrática cuja imagem de
é uma função quadrática cuja imagem de 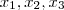 são respct.
são respct. 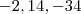 , então suponha que
, então suponha que 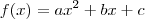 (onde ab,c são constantes a ser determinadas ) .
(onde ab,c são constantes a ser determinadas ) . 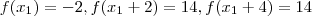 .
.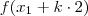 . Obterá algo do gênero
. Obterá algo do gênero 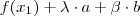 (OBS.: Não fiz a conta apenas verifiquei mentalmente o formato da expressão geral )
(OBS.: Não fiz a conta apenas verifiquei mentalmente o formato da expressão geral )
