zenildo escreveu:CALCULE A SOMA DOS 23 PRIMEIROS TERMOS DA P.A. (1;4;7;10;...)
Sabemos que uma Progressão Aritmética consiste num conjunto de números, finito ou infinito, tais que a diferença entre um e seu antecessor é uma razão. Bem, tomemos uma razão r da P.A. em questão; além disso, a1=1, a2=4, a3=7, a4=10 e assim por diante. Observe que: a2 - a1 = 4 - 1 = 3; a3 - a2 = 7 - 4 = 3; a4 - a3 = 10 - 7 = 3; e assim sucessivamente. Logo, a razão é r = 3. Para calcular o resultado da soma dos 23 primeiros números da P.A em questão, podemos usar uma fórmula ou, então pensar da seguinte maneira:
Por exemplo: qual é o resultado de 1+2+3+4+5 ? Podemos fazer assim:
1+2+3+4+5
5+4+3+2+1
---------------
6+6+6+6+6 = 6 . 5 = 30
Este resultado devemos dividir por 2 e, portanto: 30/2 = 15 = 1+2+3+4+5.
Observe que, o que eu fiz foi pensar o seguinte: se temos que saber quanto vale a soma de 1+2+3+4+5, podemos fazer aquele esqueminha que consiste em saber quanto vale a soma do primeiro termo com o último, do segundo com o penúltimo e assim por diante. Então, obtemos que 1+5=4+2=3+3=4+2=5+1=6. Contudo, obtemos 5 vezes tal valor e, portanto, obtemos o resultado 30, mas temos que dividir por 2, pois, caso contrário, estaríamos contando a soma desses números duas vezes, o que nos daria a resposta errada.
Esta é só uma maneira de pensar que, talvez, pudesse facilitar. Contudo, se não fui muito clara na explicação, aqui vai a fórmula para resolver.
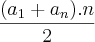
Daí, basta substituir:
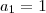
e
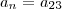
n = 23
Assim,
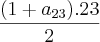
.
Contudo, quem é
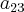
?
Basta lembrar que
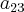
=

=
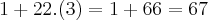
Então:

Logo, 782 é o resultado da soma dos 23 primeiros termos da P.A. em questão.
Observação: a23 = a1+22r justamente por tratar-se de uma P.A, pois temos que, por exemplo, a2=a1+r; a3=a1+2r; a4=a1+3r e assim por diante.
Ok?



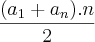
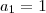 e
e 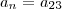
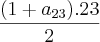 .
.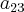 ?
?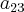 =
=  =
= 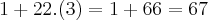


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.