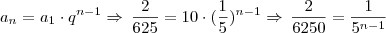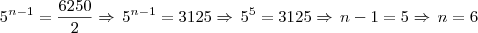por willwgo » Qui Fev 24, 2011 17:09
por willwgo » Qui Fev 24, 2011 17:09
(ufsc) na progressão geometrica (10,2,2/5,2/25,.....), qual e a posicao do termo 2/625?
me ajudem ai!
desde ja agradeço
-
willwgo
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qui Fev 17, 2011 15:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Renato_RJ » Qui Fev 24, 2011 21:14
por Renato_RJ » Qui Fev 24, 2011 21:14
Boa noite campeão... Tudo em paz ??
Vamos ver se posso lhe ajudar, você tem uma P.G. cuja razão é

e você quer a posição de

, então podemos usar:
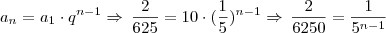
Resolvendo, teremos:
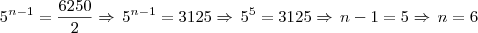
Espero que tenha ajudado...
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por willwgo » Sex Mar 11, 2011 17:08
por willwgo » Sex Mar 11, 2011 17:08
obrigado me ajudo mtooo
-
willwgo
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qui Fev 17, 2011 15:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Lucas Ambrus de lima » Sáb Jun 29, 2013 21:47
por Lucas Ambrus de lima » Sáb Jun 29, 2013 21:47
(UFSC)Na progressão geométrica(10, 2, 2/5, 2/25,...), qual é a posição do termo 2/625?
Neste problema, podemos utilizar a fórmula do termo geral:
an= a1 . q*n-1
2/625= 10 . 1/5*n-1
2/625 : 10 = 1/5*n-1
2/625 . 1/10= 1/5*n-1
2/6250= 1/5*n-1
1/3125= 1/5*n-1
1/5*5= 1/5*n-1
5 =n-1
n=6
Obs:A resposta dada pelo outro usuário está totalmente incorreta, e desprovida de sentido.
de 1/5*n-1 jamais chegaremos à 1/5n-1...
Portanto, avalie bem as respostas dadas pelos outros usuários...
-
Lucas Ambrus de lima
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Jun 29, 2013 21:32
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Alguem poderia me ajudar com esse exercicio ?
por rodrigo321 » Dom Dez 06, 2009 03:33
- 1 Respostas
- 2009 Exibições
- Última mensagem por Molina

Dom Dez 06, 2009 12:09
Cálculo: Limites, Derivadas e Integrais
-
- Alguem pode ajudar não compreendi muito bem esse exercicio
por joaoalbertotb » Ter Set 01, 2009 14:08
- 11 Respostas
- 6707 Exibições
- Última mensagem por Elcioschin

Qui Set 03, 2009 17:02
Sistemas de Equações
-
- [Geometria Analítica] Poderiam me ajudar?
por Ronaldobb » Dom Out 13, 2013 22:43
- 1 Respostas
- 1259 Exibições
- Última mensagem por Bravim

Dom Out 13, 2013 23:48
Geometria Analítica
-
- [FUNÇÃO] Poderiam me ajudar nessa questão da PUC?
por 20nho » Sáb Set 14, 2013 17:36
- 1 Respostas
- 1208 Exibições
- Última mensagem por Pessoa Estranha

Dom Set 15, 2013 12:26
Funções
-
- Poderiam me ajudar com essa regra da cadeia?
por vladimir366 » Qui Set 21, 2017 22:34
- 0 Respostas
- 1097 Exibições
- Última mensagem por vladimir366

Qui Set 21, 2017 22:34
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 e você quer a posição de
e você quer a posição de  , então podemos usar:
, então podemos usar: