 por ramonalado » Ter Mar 12, 2013 23:35
por ramonalado » Ter Mar 12, 2013 23:35
Determine a soma dos 60 primeiros termos da P.A em que
2a1 + a3 = -11
a2 -3a5 = -12
Nao intendi mt bem , mais acho que tenho que fazer em funcao de a1 tipo :
2a1 + (a1+2r) = -11
(a1+r) -(3a1+4r) = -12
-
ramonalado
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Fev 20, 2013 19:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Operador de Computador
- Andamento: cursando
 por Russman » Qua Mar 13, 2013 00:12
por Russman » Qua Mar 13, 2013 00:12
Tome
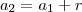
,
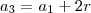
e
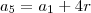
. Assim, você terá um sistema linear de equações em
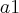
e

. Com esses dados você poderá calcular a soma.
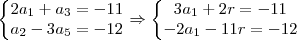
Multiplicando a 2° equação por
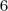
a 1° por 2 e somando-as, temos
![3[2]+2[1] = 3.(-12) + 2(-11)\Rightarrow -6a_1 - 33r + 6a_1+4r = 58\Rightarrow r=\frac{58}{-29} = -2 3[2]+2[1] = 3.(-12) + 2(-11)\Rightarrow -6a_1 - 33r + 6a_1+4r = 58\Rightarrow r=\frac{58}{-29} = -2](/latexrender/pictures/e6bf58c3d65c7b10daae624f07e6dbd7.png)
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por ramonalado » Qua Mar 13, 2013 13:50
por ramonalado » Qua Mar 13, 2013 13:50
Pq que na parte de
-2a1 - 11r = -12 ficou 11r ? e nao 4
-
ramonalado
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Fev 20, 2013 19:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Operador de Computador
- Andamento: cursando
 por Russman » Qua Mar 13, 2013 22:46
por Russman » Qua Mar 13, 2013 22:46

Certo?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Progressão geométrica] Soma dos n primeiros termos
por fff » Ter Jan 07, 2014 13:30
- 3 Respostas
- 5282 Exibições
- Última mensagem por fff

Ter Jan 07, 2014 17:47
Sequências
-
- [Progressões] Encontrar os primeiros termos
por GrazielaSilva » Sex Set 28, 2012 11:28
- 2 Respostas
- 12983 Exibições
- Última mensagem por Yokotoyota

Qui Fev 04, 2016 03:09
Progressões
-
- [Série de Taylor] 4 primeiros termos
por Crist » Sáb Mar 09, 2013 17:52
- 2 Respostas
- 10026 Exibições
- Última mensagem por Crist

Dom Mar 10, 2013 23:12
Sequências
-
- Determinar o no. de termos da PA
por Carolziiinhaaah » Qua Jun 16, 2010 21:30
- 4 Respostas
- 4125 Exibições
- Última mensagem por Tom

Ter Jul 06, 2010 00:10
Progressões
-
- Soma de termos
por apotema2010 » Sex Fev 26, 2010 17:22
- 5 Respostas
- 6298 Exibições
- Última mensagem por Cleyson007

Dom Fev 28, 2010 08:50
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



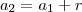 ,
, 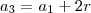 e
e 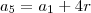 . Assim, você terá um sistema linear de equações em
. Assim, você terá um sistema linear de equações em 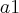 e
e  . Com esses dados você poderá calcular a soma.
. Com esses dados você poderá calcular a soma.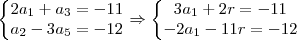
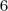 a 1° por 2 e somando-as, temos
a 1° por 2 e somando-as, temos![3[2]+2[1] = 3.(-12) + 2(-11)\Rightarrow -6a_1 - 33r + 6a_1+4r = 58\Rightarrow r=\frac{58}{-29} = -2 3[2]+2[1] = 3.(-12) + 2(-11)\Rightarrow -6a_1 - 33r + 6a_1+4r = 58\Rightarrow r=\frac{58}{-29} = -2](/latexrender/pictures/e6bf58c3d65c7b10daae624f07e6dbd7.png)




 .
.



