 por claudia_r » Ter Out 06, 2009 11:05
por claudia_r » Ter Out 06, 2009 11:05
Estou com muita dificuldade para resolver esse exercício de P.A.
Numa P.A. de primeiro termo 1/3 e razão 1/2, a soma dos n primeios termos é 20/3. Determine o valor de n.
Encontrei o segundo termo da P.A. usando a fórmula do termo geral, já que tinha os dados de a1 e da razão. Depois peguei o resultado e joguei na fórmula da soma dos termos, mas não deu certo, ficou uma conta ridícula :/
-
claudia_r
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Out 06, 2009 10:33
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por marciommuniz » Ter Out 06, 2009 13:08
por marciommuniz » Ter Out 06, 2009 13:08
A soma de uma P.A é dada por:
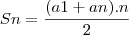
"Nunca penso no futuro, ele chega rápido demais." Albert Einsten
-
marciommuniz
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 08, 2009 20:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Metalúrgica UFF /Química Lic. UENF
- Andamento: cursando
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


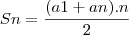


 .
.
 :
: