Depois de descobrir que poderia relacionar PA e PG com funções polinomais e exponenciais, respectivamente, achei mais proveitoso trabalhar com tais funções a aquelas fórmulas e equações de progressões que, para mim, são abomináveis! Pretendo, então, fazer algumas demonstrações...
Em primeiro lugar, é necessário saber que uma PA de 1ª ordem se corresponde com a função afim: "y=ax+b", a de 2ª ordem com a função quadrática: "y=ax²+bx+c" e assim sucessivamente... Ademais, sabemos que essas funções são relacionadas através do cálculo diferencial e integral. Derivando uma função quadrática obtem-se uma função linear... se essas funções representam progressões então podemos facilmente saltar entre as ordens das mesmas!
Jás as PG de 1ª, 2ª e 3ª ordem... se correspondem respectivamente com as seguintes funções:
 ;
;  ;
;  . Descobre-se a tx de variações dessas funções através da derivada geométrica:
. Descobre-se a tx de variações dessas funções através da derivada geométrica: ![f^*(x)=\sqrt[dx]{dy} f^*(x)=\sqrt[dx]{dy}](/latexrender/pictures/cf5394db08e05adad1730623d0b141dd.png) .
.OK! ... Mas o que o cálculo tem a ver com progressões? Tudo! Em progressões, fala-se muito em diferença e em razão entre termos consecutivos, isto é a derivada da função (progressão) avaliada na média (em x) entre os termos escolhidos. Vejam os exemplos abaixos:
Bem, eu considero isso extramamente relevante, muito embora nunca vi nem ouvi essa explicação.
E o segundo ponto que tenho a dizer é que eu determinei uma fórmula que calcula o somatório entre termos consecutivos duma função polinomial e o produtório entre termos consecutivos duma função exponencial.
Dada uma função do tipo
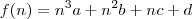 , a soma dos termos consecutivos é feita da seguinta maneira:
, a soma dos termos consecutivos é feita da seguinta maneira: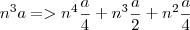
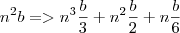
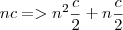

Mas como a função é
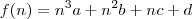 , então implica que o somatório dos termos consecutivos é:
, então implica que o somatório dos termos consecutivos é:
E para a função do tipo
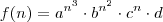 , o produtório entre os termos consecutivos é feito da seguinda maneira:
, o produtório entre os termos consecutivos é feito da seguinda maneira:![a^{n^3}=>\sqrt[4]{a}^{n^4}\cdot\sqrt[2]{a}^{n^3}\cdot\sqrt[4]{a}^{n^2} a^{n^3}=>\sqrt[4]{a}^{n^4}\cdot\sqrt[2]{a}^{n^3}\cdot\sqrt[4]{a}^{n^2}](/latexrender/pictures/ce313bb767354176731abb61d500dbf3.png)
![b^{n^2}=>\sqrt[3]{b}^{n^3}\cdot\sqrt[2]{b}^{n^2}\cdot\sqrt[6]{b}^n b^{n^2}=>\sqrt[3]{b}^{n^3}\cdot\sqrt[2]{b}^{n^2}\cdot\sqrt[6]{b}^n](/latexrender/pictures/a7ed637bdee3e96deb47cc2bd4c2a913.png)
![c^n=>\sqrt[2]{c}^{n^2}\cdot\sqrt[2]{c}^n c^n=>\sqrt[2]{c}^{n^2}\cdot\sqrt[2]{c}^n](/latexrender/pictures/2d3ab81af46c7b5ae4bf8d556a116d52.png)
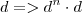
Mas como a função é
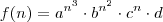 , então implica que o produtório dos termos consecutivos é totalmente análogo ao método do polinômio.
, então implica que o produtório dos termos consecutivos é totalmente análogo ao método do polinômio.Fonte: Eu.
O que acham?
Até mais,


 uma variável discreta e
uma variável discreta e 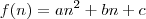 uma função desta variável.
uma função desta variável. de
de  , isto é, você está calculando a diferença de termos consecutivos e afirma que
, isto é, você está calculando a diferença de termos consecutivos e afirma que 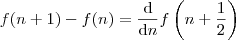
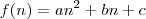
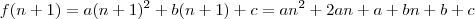
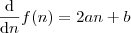


 , então podemos afirmar que existe a identidade dada por
, então podemos afirmar que existe a identidade dada por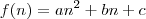 .
.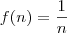 e comecei a ter sérias dificuldades. Então comecei a averiguar o problema e notei através do Geogebra que "a diferença entre termos consecutivos duma função é igual a sua derivada avaliada na média (em x) destes termos" não parece ser verdadeira para as funções de grandezas inversas, por exemplo:
e comecei a ter sérias dificuldades. Então comecei a averiguar o problema e notei através do Geogebra que "a diferença entre termos consecutivos duma função é igual a sua derivada avaliada na média (em x) destes termos" não parece ser verdadeira para as funções de grandezas inversas, por exemplo:




