 por JU201015 » Dom Nov 18, 2012 11:52
por JU201015 » Dom Nov 18, 2012 11:52
Uma progressão geométrica crescente é formada por três termos positivos cujo produto é 1. Determine essa PG, sabendo que a soma dos três termos é 21/4.
Ok. Então:
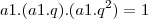
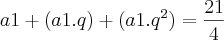
Mas não sei como se desenvolve essa conta. Me ajudem?
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Dom Nov 18, 2012 12:20
por young_jedi » Dom Nov 18, 2012 12:20
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por JU201015 » Dom Nov 18, 2012 13:17
por JU201015 » Dom Nov 18, 2012 13:17
Não entendi pq de
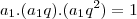
passou para

.
E nem porque desta

passou para a próxima

=s
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por JU201015 » Dom Nov 18, 2012 19:32
por JU201015 » Dom Nov 18, 2012 19:32
young_jedi escreveu: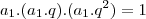
como são multiplicações eu posso escrever assimm
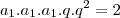
apenas alterei a ordem do fatores o produto continua sendo o mesmo

tambem posso colocar o expoente em evidencia
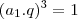
tirando a raiz cubica da dos dois lados da equação
![a_1.q=\sqrt[3]1 a_1.q=\sqrt[3]1](/latexrender/pictures/2080b714c666357cc4a5a765fa50b575.png)



Multiplica por q:



E assim, a razão fica sendo 4 porque se fosse 1/4 seria decrescente sendo que no enunciado diz que a progressão é crescente, certo?
Se a razão é 4, então a1 é 1/4.
PG=(1/4; 1; 4).
Está correto?
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Dom Nov 18, 2012 19:45
por young_jedi » Dom Nov 18, 2012 19:45
correto, é isso ai mesmo!!
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por JU201015 » Dom Nov 18, 2012 21:02
por JU201015 » Dom Nov 18, 2012 21:02
young_jedi escreveu:correto, é isso ai mesmo!!
Mto obrigada mesmo pela assistência =D
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Progressao] série geometrica X progressao geometrica?
por aajunim » Seg Mar 18, 2013 11:19
- 2 Respostas
- 4252 Exibições
- Última mensagem por aajunim

Ter Mar 19, 2013 11:44
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4725 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- Progressão geométrica (ITA)
por Ananda » Sex Mar 07, 2008 13:27
- 17 Respostas
- 25545 Exibições
- Última mensagem por Ananda

Qui Mar 13, 2008 11:10
Progressões
-
- Progressão Geométrica
por nicecaps » Seg Mar 22, 2010 11:37
- 2 Respostas
- 4234 Exibições
- Última mensagem por nicecaps

Ter Mar 23, 2010 09:45
Progressões
-
- Progressão Geométrica
por Jessie » Qui Abr 29, 2010 17:49
- 1 Respostas
- 2889 Exibições
- Última mensagem por Elcioschin

Qui Abr 29, 2010 20:12
Pedidos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
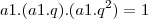
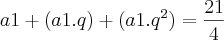

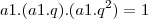
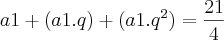

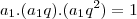


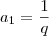

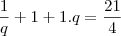

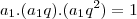 passou para
passou para  .
. passou para a próxima
passou para a próxima  =s
=s
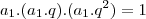
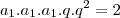

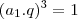
![a_1.q=\sqrt[3]1 a_1.q=\sqrt[3]1](/latexrender/pictures/2080b714c666357cc4a5a765fa50b575.png)















