 por Rafael16 » Sáb Jul 28, 2012 17:04
por Rafael16 » Sáb Jul 28, 2012 17:04
Boa tarde pessoal!
(Cesesp-PE) Dois andarilhos iniciam juntos uma caminhada. Um deles caminha uniformemente 10 km por dia e o outro caminha 8 km no primeiro dia e acelera o passo de modo a caminhar mais 0,5 km a cada dia que se segue. Assinale a alternativa correspondente ao número de dias caminhados para que o segundo andarilho alcance o primeiro.
(a) 10 (b) 9 (c) 3 (d) 5 (e) 21
Minha resolução:
(I) (10,20,30...)
(II)(8,33/2,...) encontrei a razão como sendo r = 17/2
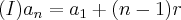
Substituindo os valores, achei:
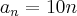
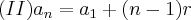
Substituindo os valores:
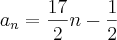
Igualei (I) com (II) para achar n, que é o número de dias para alcançar o primeiro:
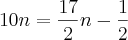

Não entendi se minha conta esta errada, ou se é meu raciocínio...
Gostaria que me explicasse isso, valeu!
Resposta: b
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por e8group » Sáb Jul 28, 2012 21:59
por e8group » Sáb Jul 28, 2012 21:59
Acho que isso aqui resolve seu exercício ,
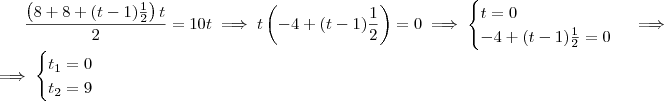
,
portanto t = 9 dias .
OBS.:
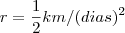
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Seg Jul 30, 2012 01:43
por Russman » Seg Jul 30, 2012 01:43
O seu problema pode ser resolvido interpretando-o como cinemático!
Sejam
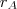
e
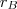
as posições relativas a um referencial inercial dos andarilhos, medidas em km, e

um parâmetro, medido em dias.
Rafael16 escreveu:Dois andarilhos iniciam juntos uma caminhada.
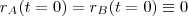
.
Rafael16 escreveu:Um deles caminha uniformemente 10 km por dia
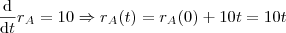
Rafael16 escreveu:e o outro caminha 8 km no primeiro dia e acelera o passo de modo a caminhar mais 0,5 km a cada dia que se segue.
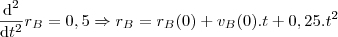

No encontro, teremos

. Assim,
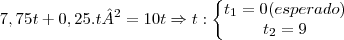
.
Assim, eles encontram-se no final do 9 dia.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Seg Jul 30, 2012 02:05
por Russman » Seg Jul 30, 2012 02:05
Você não pode interpretar a questão como um problema de Progressão Aritmética, pelo menos para o 2° andarilho, pois não é verdade este fato.
Veja que o segundo andarilho tem uma equação recorrente em suas posições de forma que
A(n+1) - A(n) = 0,5n
A(1) = 8
A(0)=0
enquanto que uma P.A. segue a equação
A(n+1) - A(n) = r.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
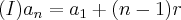
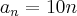
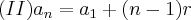
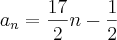
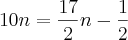



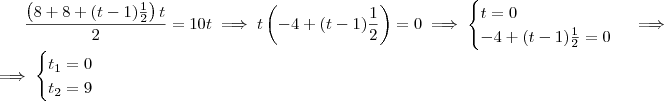 ,
,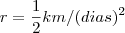
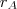 e
e 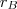 as posições relativas a um referencial inercial dos andarilhos, medidas em km, e
as posições relativas a um referencial inercial dos andarilhos, medidas em km, e  um parâmetro, medido em dias.
um parâmetro, medido em dias.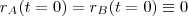 .
.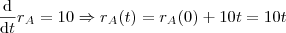
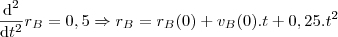

 . Assim,
. Assim, 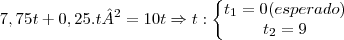 .
.




