 por LuRodrigues » Dom Abr 22, 2012 20:08
por LuRodrigues » Dom Abr 22, 2012 20:08
Caros,
Gostaria de contar com auxílio na resolução:
De uma sequência infinita de quadrados onde a medida do lado de cada um, a partir do segundo é sempre a metade da medida do lado do quadrado anterior, sabe-se que o lado do primeiro quadrado mede 8. Calcular a soma das áreas.
Eu fiz o seguinte cálculo:
a1=8
q=1/2
Aplicando na fórmula de PG infinita=> 16
R: S= l x l => 156
Porém, como resposta conta 145/3 - não entendi a origem do "3". Poderiam me ajudar?
Obrigada.
-
LuRodrigues
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Abr 22, 2012 19:03
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
 por LuRodrigues » Dom Abr 22, 2012 20:10
por LuRodrigues » Dom Abr 22, 2012 20:10
Somente retificando a resposta da área que encontrei: 256
Mas como resposta consta 256/3
-
LuRodrigues
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Abr 22, 2012 19:03
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
 por DanielFerreira » Ter Mai 01, 2012 00:51
por DanielFerreira » Ter Mai 01, 2012 00:51
LuRodrigues escreveu:Caros,
Gostaria de contar com auxílio na resolução:
De uma sequência infinita de quadrados onde a medida do lado de cada um, a partir do segundo é sempre a metade da medida do lado do quadrado anterior, sabe-se que o lado do primeiro quadrado mede 8. Calcular a soma das áreas.
Eu fiz o seguinte cálculo:
a1=8
q=1/2
Aplicando na fórmula de PG infinita=> 16
R: S= l x l => 156
Porém, como resposta conta 145/3 - não entendi a origem do "3". Poderiam me ajudar?
Obrigada.
O lado do 1º quadrado mede 8, então sua área é 64;
O lado do 2º quadrado mede 4, então sua área é 16;
O lado do 3º quadrado mede 2, então sua área é 4;
(...)
Deixemos os lados de 'lado' e trabalhemos com as áreas:


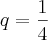
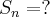
Sabe-se que:
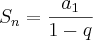
então,
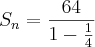
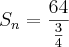

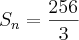
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- áreas
por cristina » Sex Abr 16, 2010 10:50
- 1 Respostas
- 1721 Exibições
- Última mensagem por Neperiano

Ter Set 27, 2011 19:56
Geometria Plana
-
- AREAS DE FIGURAS
por JOHNY » Qui Set 02, 2010 18:17
- 1 Respostas
- 1970 Exibições
- Última mensagem por Douglasm

Qui Set 02, 2010 18:48
Geometria Plana
-
- Problemas com áreas
por PikenaPin » Ter Mai 31, 2011 14:54
- 1 Respostas
- 2224 Exibições
- Última mensagem por guermandi

Qua Jun 01, 2011 15:22
Geometria Plana
-
- [QUADRILÁTEROS]ÁREAS
 por anabrizola » Seg Ago 05, 2013 22:31
por anabrizola » Seg Ago 05, 2013 22:31
- 0 Respostas
- 1533 Exibições
- Última mensagem por anabrizola

Seg Ago 05, 2013 22:31
Geometria Plana
-
- Integral - áreas
por Danilo » Sáb Nov 09, 2013 18:42
- 1 Respostas
- 2130 Exibições
- Última mensagem por e8group

Sex Nov 15, 2013 11:44
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




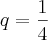
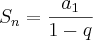
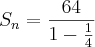
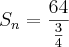

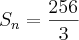

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
