
para n=1
fica 10=10
hip. ind.
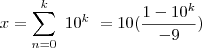
tese k+1
[tex]x=\sum_{n=0}^n \ 10^k^+^1 \ = 10 (\frac{1-10^k^+^1)} {-9} )[/tex
a partir daqui não sei o que fazer :(
Obrigado.


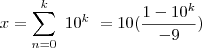

TiagoFERD escreveu:

TiagoFERD escreveu:para n=1
fica 10=10
TiagoFERD escreveu:hip. ind.

TiagoFERD escreveu:tese k+1
a partir daqui não sei o que fazer :(
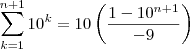
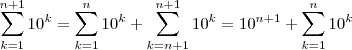

LuizAquino escreveu:TiagoFERD escreveu:
Do jeito que está, essa relação é falsa. O correto seria:TiagoFERD escreveu:para n=1
fica 10=10
Ok, desde que considere a relação que citei acima.TiagoFERD escreveu:hip. ind.
A hipótese correta seria:TiagoFERD escreveu:tese k+1
a partir daqui não sei o que fazer :(
A tese seria:
Comece fazendo o seguinte:
Agora use a hipótese de indução.

TiagoFERD escreveu:Obrigado mas eu desisto não consigo mesmo fazer isso. :(

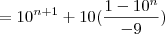


TiagoFERD escreveu:Ora,
e desenvolvo até o fim?
 é igual a
é igual a  , e não
, e não  como você escreveu.
como você escreveu.


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)