gostaria da ajuda, se possível, na resolução dessa questão do ITA.
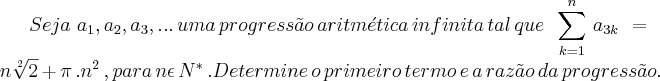
Tentei resolvê-la adotando valores para o k, como de costume. Para k=1, achei
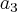 , adotando esse como sendo a soma de
, adotando esse como sendo a soma de  . Novamente, adotei k=2 e achei
. Novamente, adotei k=2 e achei  , em seguida adotei o mesmo pensamento anterior. A partir daí adotei o conceito de PA nas duas equações, resolvi o sistema e consegui achar o que foi pedido.
, em seguida adotei o mesmo pensamento anterior. A partir daí adotei o conceito de PA nas duas equações, resolvi o sistema e consegui achar o que foi pedido.Entretanto, minha resposta está diferente da do livro.
Achei:
![r=2\pi\:e\:a{}_{1}=\sqrt[]{2}+\pi r=2\pi\:e\:a{}_{1}=\sqrt[]{2}+\pi](/latexrender/pictures/de113ebac6bc53549d5e6a4705a155e0.png) .
.Sendo a resposta:
![a{}_{1}=\sqrt[]{2}-\frac{\pi}{3}\:e\:r=\frac{2\pi}{3} a{}_{1}=\sqrt[]{2}-\frac{\pi}{3}\:e\:r=\frac{2\pi}{3}](/latexrender/pictures/1f19568758db998227acae19e2f0bc7a.png)
Obrigada pela ajuda,
Jéssica.


 , para
, para  .
.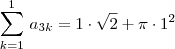





 , então
, então 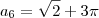 .
.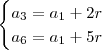


 .
.



