 por fernandocez » Sex Fev 25, 2011 20:23
por fernandocez » Sex Fev 25, 2011 20:23
Caros amigos, eu não consigo responder essa pergunta:
51. Em uma progressão geométrica, o segundo termo é
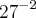
e o terceiro termo é
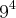
. Então, o quinto termo é:
resposta:
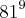
Eu tentei pela fórmula:
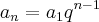

=?
q=?
n=5
Eu acho que bastava achar a razão (q) assim ia multiplicando até achar o quinto termo. Só que não consegui achar uma razão. Aguardo a ajuda.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por Molina » Sex Fev 25, 2011 21:15
por Molina » Sex Fev 25, 2011 21:15
Boa noite, Fernando.
A fórmula que você quer usar precisa saber o valor do primeiro termo da progressão, como você pode perceber. Então, primeiramente descubra a razão q, dividindo o terceiro termo pelo segundo. Obtendo este valor basta dividir o segundo termo por esta razão para ter acesso ao primeiro termo. Pronto! Agora você já tem o valor do primeiro termo, basta continuar substituido na fórmula como você estava fazendo para descobrir o valor do quinto termo.
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por fernandocez » Sex Fev 25, 2011 23:45
por fernandocez » Sex Fev 25, 2011 23:45
Valeu a dica, consegui resolver. Dividi o 3º termo pelo 2º e encontrei a razão (q) como vc falou, dividi o 2º termo pela razão e encontrei o 1º termo. Usei a fórmula e encontrei a resposta (5º termo). Eu preciso passar nesse concurso para o magistério no RJ. Tá difícil arrumar emprego em colégio particular visto que não tenho experiência. Obrigado pela ajuda.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por Molina » Sáb Fev 26, 2011 13:08
por Molina » Sáb Fev 26, 2011 13:08
Boa sorte no concurso, Fernando.
Conte conosco sempre que precisar, estamos aqui para isso!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Fração] Concurso magistério 2008
por fernandocez » Dom Jul 08, 2012 19:12
- 2 Respostas
- 2155 Exibições
- Última mensagem por fernandocez

Dom Jul 08, 2012 21:15
Álgebra Elementar
-
- Questão prova magisterio 2008
por fernandocez » Seg Fev 14, 2011 16:42
- 4 Respostas
- 3033 Exibições
- Última mensagem por LuizAquino

Ter Fev 15, 2011 20:10
Polinômios
-
- Questão prova magisterio 2008
 por fernandocez » Sáb Fev 26, 2011 11:39
por fernandocez » Sáb Fev 26, 2011 11:39
- 3 Respostas
- 2400 Exibições
- Última mensagem por LuizAquino

Sáb Fev 26, 2011 19:15
Geometria Plana
-
- [trigonometria] concurso magistério 2007 (33)
por fernandocez » Sex Dez 20, 2013 09:27
- 2 Respostas
- 1961 Exibições
- Última mensagem por fernandocez

Sáb Dez 21, 2013 16:38
Trigonometria
-
- Questão prova magisterio 2007
 por fernandocez » Seg Fev 14, 2011 17:21
por fernandocez » Seg Fev 14, 2011 17:21
- 1 Respostas
- 1422 Exibições
- Última mensagem por LuizAquino

Seg Fev 14, 2011 19:57
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
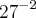 e o terceiro termo é
e o terceiro termo é 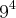 . Então, o quinto termo é:
. Então, o quinto termo é: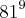
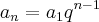
 =?
=?




 , avisa que eu resolvo.
, avisa que eu resolvo.

