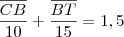por Pri Ferreira » Qua Mar 21, 2012 13:58
por Pri Ferreira » Qua Mar 21, 2012 13:58
João se desloca diariamente de sua casa (ponto C) até o
trabalho (ponto T), passando pelo (ponto B) em trajetórias
retilíneas.
Considere-se que, num determinado dia, João percorreu:
- a distância CB, com velocidade média de 10 km/h;
- a distância BT = 12 km, com velocidade média de
15 km/h.
- toda essa trajetória em 1h30min.
Se o seno do ângulo CBT vale 0,54, o segmento CA,
perpendicular à reta AT, mede, em km:
(A) 3,78
(B) 3,29
(C) 2,56
(D) 2,14
Urgente!!!
-
Pri Ferreira
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Qua Out 19, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por LuizAquino » Sáb Mar 31, 2012 15:20
por LuizAquino » Sáb Mar 31, 2012 15:20
Pri Ferreira escreveu:João se desloca diariamente de sua casa (ponto C) até o
trabalho (ponto T), passando pelo (ponto B) em trajetórias
retilíneas.
Considere-se que, num determinado dia, João percorreu:
- a distância CB, com velocidade média de 10 km/h;
- a distância BT = 12 km, com velocidade média de
15 km/h.
- toda essa trajetória em 1h30min.
Se o seno do ângulo CBT vale 0,54, o segmento CA,
perpendicular à reta AT, mede, em km:
(A) 3,78
(B) 3,29
(C) 2,56
(D) 2,14
O texto do exercício está mal posto. Ele deveria informar que A está sobre o segmento BT.
Considerando que A esteja sobre BT, a figura abaixo ilustra o exercício.
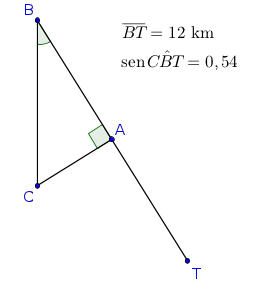
- figura.png (9.62 KiB) Exibido 1246 vezes
Note que 1h30min é o mesmo que 1,5 horas. Desse modo, temos que:
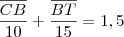
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12994 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10976 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 15117 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
-
- Questão da FCC
por wanderlymarques » Qua Nov 18, 2009 12:44
- 2 Respostas
- 5034 Exibições
- Última mensagem por wanderlymarques

Qui Nov 19, 2009 12:58
Cálculo: Limites, Derivadas e Integrais
-
- questão
por sirle ignes » Seg Mar 08, 2010 23:46
- 2 Respostas
- 4803 Exibições
- Última mensagem por sirle ignes

Ter Mar 09, 2010 17:32
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.