 por Joseaugusto » Ter Mar 06, 2012 11:43
por Joseaugusto » Ter Mar 06, 2012 11:43
Um amigo me passou um exercício e por nada nesse mundo eu consigo resolvê-lo:

o raciocínio que tive até aqui (chamei o alfa de x para facilitar a escrita):
a² = 2 - 2cosx
b² = 2 - 2cos(2x)
onde:
cos²(2x) = cos²(x +x) = cos²x - sen²x
portanto:
b² = 2 - 2(cos²x - sen²x)
da relação fundamental da trigonometria:
b² = 2 - 2[cos²x - (1-cos²x)]
b² = 2 - 2(2cos²x -1)
b² = 2 - 4cos²x -2
b² = 4 - 4cos²x
(b/a)² = 4(1 - cos²x) / 2(1 - cosx)
simplificando:
(b/a)² = 2(1 - cos²x) / (1 - cosx)
mas 1 -cos²x é um produto notável: (1 - cosx)(1 + cosx)
(b/a)² = 2(1 - cosx)(1 + cosx) / (1 - cosx)
(b/a)² = 2(1 + cosx)
portanto:
![\frac{b}{a} = \sqrt[2]{2(1 + cosx)} \frac{b}{a} = \sqrt[2]{2(1 + cosx)}](/latexrender/pictures/ec29823a25354d05b3febcfdd8984f13.png)
e travei aqui. Ja estou a mais de duas horas nesse exercicio e não consigo avançar

Alguma luz?
-
Joseaugusto
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Mar 06, 2012 11:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Ter Mar 06, 2012 15:53
por MarceloFantini » Ter Mar 06, 2012 15:53
Não encontro erros na sua resolução. De onde é?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Ter Mar 06, 2012 15:54
por LuizAquino » Ter Mar 06, 2012 15:54
Joseaugusto escreveu:portanto:
![\frac{b}{a} = \sqrt[2]{2(1 + cosx)} \frac{b}{a} = \sqrt[2]{2(1 + cosx)}](/latexrender/pictures/ec29823a25354d05b3febcfdd8984f13.png)
e travei aqui. Ja estou a mais de duas horas nesse exercicio e não consigo avançar
Alguma luz?
Dica: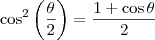
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fraol » Ter Mar 06, 2012 17:21
por fraol » Ter Mar 06, 2012 17:21
Com essa dica fica fácil.
(tb sai pela Lei dos Senos).
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Joseaugusto » Ter Mar 06, 2012 22:42
por Joseaugusto » Ter Mar 06, 2012 22:42
nossa, com a lei dos senos fica bem fácil, mesmo. Obrigado a todos

-
Joseaugusto
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Mar 06, 2012 11:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Lei dos cossenos
por kandara » Qua Abr 30, 2014 17:35
- 1 Respostas
- 4567 Exibições
- Última mensagem por Russman

Qua Abr 30, 2014 18:54
Trigonometria
-
- UFSCar - Lei dos cossenos
por brunocav » Seg Mai 30, 2011 18:16
- 2 Respostas
- 10556 Exibições
- Última mensagem por brunocav

Seg Mai 30, 2011 19:23
Trigonometria
-
- LEI DOS SENOS E COSSENOS
por MERLAYNE » Qua Abr 25, 2012 20:36
- 1 Respostas
- 1816 Exibições
- Última mensagem por Russman

Qua Abr 25, 2012 21:26
Trigonometria
-
- Multiplicação de cossenos
por anfran1 » Sex Jun 29, 2012 10:39
- 5 Respostas
- 5166 Exibições
- Última mensagem por Arkanus Darondra

Dom Jul 01, 2012 12:48
Álgebra Elementar
-
- LEI dos COSSENOS PROBLEMA
 por emarga » Sex Out 26, 2018 16:52
por emarga » Sex Out 26, 2018 16:52
- 2 Respostas
- 3277 Exibições
- Última mensagem por emarga

Qua Nov 07, 2018 17:49
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![\frac{b}{a} = \sqrt[2]{2(1 + cosx)} \frac{b}{a} = \sqrt[2]{2(1 + cosx)}](/latexrender/pictures/ec29823a25354d05b3febcfdd8984f13.png)





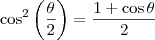


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
