Olá Brunna, boa tarde, seja bem-vinda!
Acredito que você tenha lido as regras do fórum.
Entendo sua necessidade para entrega, mas o objetivo aqui não é simplesmente fornecer a resolução, mas sim, interagir a partir das dúvidas, tentativas e dificuldades, visando colaborar com o estudo e entendimento alheio.
Neste contexto, caso queira ajuda sobre "como começar", seguem algumas dicas.
Em primeiro lugar, ao falarmos de círculo trigonométrico e funções trigonométricas, é preciso ter em mente suas representações, utilizando triângulos semelhantes. Eu preparei uma figura do círculo unitário, reunindo as medidas das funções:
As relações trigonométricas são provenientes da semelhança entre os triângulos retângulos.
Repare que algumas delas são aplicações diretas do teorema de Pitágoras, veja e compare com a figura:

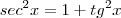
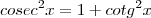
Veja abaixo como relações mais comuns como a tangente e secante são obtidas por semelhança.
Para a tangente, partimos da semelhança entre os triângulos OAF e OBC, pelo caso ângulo-ângulo:
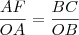
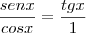
De onde segue:

A secante, utilizada no cálculo pelo
molina, tem origem da semelhança entre os mesmos triângulos OAF e OBC, compare localizando na figura:
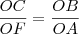

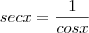
Brunna, note que o ângulo x nesta figura está no primeiro quadrante, mas as relações são válidas para os quatro quadrantes.
Convém utilizar a idéia desta construção para fazer a sua figura no terceiro quadrante, só assim você visualizará o que está calculando.
De qualquer forma, apenas com o que foi apresentado aqui, você já pode exercitar os cálculos pedidos utilizando as relações.
Comente suas dúvidas e bons estudos!
Espero ter ajudado.





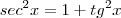
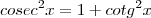
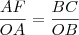
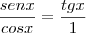

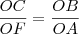

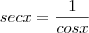



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.