 por Thiago1986Iz » Qua Jul 13, 2016 08:48
por Thiago1986Iz » Qua Jul 13, 2016 08:48
Saudações
Estou com uma dúvida na resolução de uma equação trigonométrica,
![sen x= \frac{-\sqrt[2]{2}}{2}\Rightarrow sen\frac{5\pi}{4} sen x= \frac{-\sqrt[2]{2}}{2}\Rightarrow sen\frac{5\pi}{4}](/latexrender/pictures/1debd6e0796e5ffde8ca926581a18412.png)
, minha dúvida é: eu sei que para o seno dar igual a
![\frac{\sqrt[2]{2}}{2} \frac{\sqrt[2]{2}}{2}](/latexrender/pictures/087ef0498ec0056debd92518bfa3944e.png)
o ângulo tem que ser igual a

, mas para dar
![\frac{-\sqrt[2]{2}}{2} \frac{-\sqrt[2]{2}}{2}](/latexrender/pictures/12324116d725a31413a238fac687fa68.png)
o ângulo tem que ser igual a

, como eu faço para achar esse ângulo
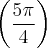
?
-
Thiago1986Iz
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Mai 27, 2016 22:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia química
- Andamento: cursando
 por DanielFerreira » Qua Jul 13, 2016 21:04
por DanielFerreira » Qua Jul 13, 2016 21:04
Olá Thiago, boa noite!!
Na verdade, o ângulo deve ser igual a

.
Se você somar

à

, irá obter
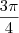
cujo o seno também será
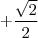
, pois o seno também é positivo no segundo quadrante. Desse modo, deverá somar

.
Dê uma olhada na função seno.
Espero ter ajudado!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Thiago1986Iz » Dom Jul 17, 2016 11:21
por Thiago1986Iz » Dom Jul 17, 2016 11:21
Obrigado.
-
Thiago1986Iz
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Mai 27, 2016 22:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia química
- Andamento: cursando
 por Wade » Qua Mai 03, 2017 15:50
por Wade » Qua Mai 03, 2017 15:50
Olá, estou estudando para uma bolsa de estudos, mas esqueci muita coisa do ensino médio. Eis a questão:
cos2x + cosx = 0 (0<_ x <_ 2pi). x=?
Eu sei que é simples, tenho até a resolução, mas não entendo nada. Na verdade, não tive muito de trigonometria nem no fundamental, nem no Ensino Médio. Se puderem me informar pelo menos por que tópicos devo começar, já ajudaria muito.
Abraços!
-
Wade
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Mai 03, 2017 15:42
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações] Me ajudem nessas equações do meu trabalho!
por henriquea92 » Sáb Jun 01, 2013 15:53
- 0 Respostas
- 3153 Exibições
- Última mensagem por henriquea92

Sáb Jun 01, 2013 15:53
Equações
-
- [Equações] Determinar Frações de equações
por fenixxx » Ter Fev 28, 2012 21:28
- 2 Respostas
- 4148 Exibições
- Última mensagem por fenixxx

Qua Fev 29, 2012 17:08
Funções
-
- Equações cartesianas e equações paramétricas
por Victor Mello » Sáb Ago 23, 2014 16:24
- 1 Respostas
- 3427 Exibições
- Última mensagem por Russman

Sáb Ago 23, 2014 18:29
Funções
-
- Equações
por Neperiano » Qua Fev 11, 2009 12:33
- 6 Respostas
- 6489 Exibições
- Última mensagem por marcio silva

Sex Mar 20, 2009 20:15
Sistemas de Equações
-
- Equações
por Luna » Qui Set 10, 2009 19:30
- 2 Respostas
- 2266 Exibições
- Última mensagem por Luna

Sex Set 11, 2009 19:54
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![sen x= \frac{-\sqrt[2]{2}}{2}\Rightarrow sen\frac{5\pi}{4} sen x= \frac{-\sqrt[2]{2}}{2}\Rightarrow sen\frac{5\pi}{4}](/latexrender/pictures/1debd6e0796e5ffde8ca926581a18412.png) , minha dúvida é: eu sei que para o seno dar igual a
, minha dúvida é: eu sei que para o seno dar igual a ![\frac{\sqrt[2]{2}}{2} \frac{\sqrt[2]{2}}{2}](/latexrender/pictures/087ef0498ec0056debd92518bfa3944e.png) o ângulo tem que ser igual a
o ângulo tem que ser igual a  , mas para dar
, mas para dar ![\frac{-\sqrt[2]{2}}{2} \frac{-\sqrt[2]{2}}{2}](/latexrender/pictures/12324116d725a31413a238fac687fa68.png) o ângulo tem que ser igual a
o ângulo tem que ser igual a  , como eu faço para achar esse ângulo
, como eu faço para achar esse ângulo 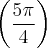 ?
?
![sen x= \frac{-\sqrt[2]{2}}{2}\Rightarrow sen\frac{5\pi}{4} sen x= \frac{-\sqrt[2]{2}}{2}\Rightarrow sen\frac{5\pi}{4}](/latexrender/pictures/1debd6e0796e5ffde8ca926581a18412.png) , minha dúvida é: eu sei que para o seno dar igual a
, minha dúvida é: eu sei que para o seno dar igual a ![\frac{\sqrt[2]{2}}{2} \frac{\sqrt[2]{2}}{2}](/latexrender/pictures/087ef0498ec0056debd92518bfa3944e.png) o ângulo tem que ser igual a
o ângulo tem que ser igual a  , mas para dar
, mas para dar ![\frac{-\sqrt[2]{2}}{2} \frac{-\sqrt[2]{2}}{2}](/latexrender/pictures/12324116d725a31413a238fac687fa68.png) o ângulo tem que ser igual a
o ângulo tem que ser igual a  , como eu faço para achar esse ângulo
, como eu faço para achar esse ângulo 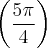 ?
?
 .
.  à
à  , irá obter
, irá obter 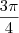 cujo o seno também será
cujo o seno também será 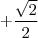 , pois o seno também é positivo no segundo quadrante. Desse modo, deverá somar
, pois o seno também é positivo no segundo quadrante. Desse modo, deverá somar  .
.







