Gostaria de confirmar uma resposta!
O exercício é:
No intervalo
 , a equação
, a equação![\sqrt[]{1 - {sen}^{2}x} + cosx = - \sqrt[]{2} \sqrt[]{1 - {sen}^{2}x} + cosx = - \sqrt[]{2}](/latexrender/pictures/66cfc5cfae955058fcc408c85cf522ee.png)
A resposta do livro é: não admite solução
Mas eu acho que é: admite como solução
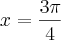
Eu fiz assim:
![\sqrt[]{{cos}^{2}x} + cosx = - \sqrt[]{2} \sqrt[]{{cos}^{2}x} + cosx = - \sqrt[]{2}](/latexrender/pictures/bda803f69f0e6db205a9a85df14f5f44.png)
![cosx + cosx = - \sqrt[]{2} cosx + cosx = - \sqrt[]{2}](/latexrender/pictures/f9143e5f2d75ecc94f2b510b153fc539.png)
![cosx = - \frac{\sqrt[]{2}}{2} cosx = - \frac{\sqrt[]{2}}{2}](/latexrender/pictures/ad19c7ad5d6f6a25c027d3afb1a2ab87.png)
E no intervalo em que a equação está, a única resposta seria
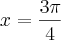
Grata desde já!

 , a equação
, a equação![\sqrt[]{1 - {sen}^{2}x} + cosx = - \sqrt[]{2} \sqrt[]{1 - {sen}^{2}x} + cosx = - \sqrt[]{2}](/latexrender/pictures/66cfc5cfae955058fcc408c85cf522ee.png)
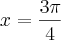
![\sqrt[]{{cos}^{2}x} + cosx = - \sqrt[]{2} \sqrt[]{{cos}^{2}x} + cosx = - \sqrt[]{2}](/latexrender/pictures/bda803f69f0e6db205a9a85df14f5f44.png)
![cosx + cosx = - \sqrt[]{2} cosx + cosx = - \sqrt[]{2}](/latexrender/pictures/f9143e5f2d75ecc94f2b510b153fc539.png)
![cosx = - \frac{\sqrt[]{2}}{2} cosx = - \frac{\sqrt[]{2}}{2}](/latexrender/pictures/ad19c7ad5d6f6a25c027d3afb1a2ab87.png)
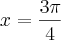

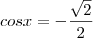 , você estaria certa, pois, de fato, no intervalo
, você estaria certa, pois, de fato, no intervalo  ,
,  deveria ser sim
deveria ser sim 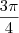 .
.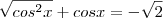

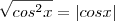
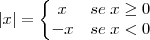
 , o sinal é indiferente, portanto, também pode ser assim:
, o sinal é indiferente, portanto, também pode ser assim: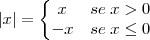
O problema ao escreveré que apenas um caso é considerado:
.
E este, o intervalo do enunciado não permite.
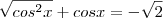

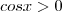
 .
.


 .
.

Mais informações sobre o projeto: http://www.cepa.if.usp.br/e-calculo

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

