Senhores, estava resolvendo uma questão de trigonometria e me deparei com essa situação.
E podia cortar uns membros da equação, mas faltavam soluções na resposta.
Citarei o exemplo com o intervalo [o, 2pi]
(1-tgx)(1+sen2x)=1+tgx
[(cosx-senx)/cosx](1+sen2x)]=(senx+cosx)/cosx
Corta o cosx.
(cosx-senx)(1+sen2x)=(senx+cosx)
(1+sen2x)²=(senx+cosx)²/(cosx-senx)²
1+2.sen2x+sen²2x=(1+sen2x)/(1-sen2x)
(1-sen2x)(1+2.sen2x+sen²2x)=(1+sen2x)
1+2sen2x+sen²2x-sen2x-2.sen²2x-sen³2x=1+sen2x
sen2x=t
-t²-t³=0
t²+t³=0
t²(1+t)=0
t=0 ou t=-1
sen2x=0 <=> sen2x=sen0 => 2x=2kpi <=> x=kpi ou 2x=pi+2kpi <=> x=pi/2 + kpi
sen2x=-1 <=> sen2x=sen3pi/2 => 2x=3pi/2+2kpi <=> x=3pi/4+kpi ou x=-pi/4+kpi
Para k=0 => x=0, ou x=pi/2, ou x=3pi/4,
Para k=1 => x=pi, ou x=3pi/2, ou x=7pi/4
S={0, pi/2, 3pi/4, pi, 3pi/2, 7pi/4}, que por sinal está errado.
Resolvendo a mesma questão
(1-tgx)(1+sen2x)=(1+tgx)
1+sen2x=(senx+cosx)/(cosx-senx)
(senx+cosx)²=(senx+cosx)/(cosx-senx)
(senx+cosx)(cosx-senx)=1
Daí a resposta continua errada.
O gabarito é S={3pi/4, 7pi/4, 0, pi, 2pi}



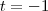 mas sim
mas sim  (no exemplo citado pelo Elcio).
(no exemplo citado pelo Elcio).


 .
.



