 por Lana Brasil » Qui Abr 17, 2014 21:44
por Lana Brasil » Qui Abr 17, 2014 21:44
Boa Noite.
Sabendo que 2 sen x + 5 cos x = 0 e que pi/2<x<pi, obtenha o valor de sen x e cos x.
Estou com dúvidas na resolução da equação acima. Resolvi cheguei a um número muito estranho para cosx e sen x mas no enunciado o intervalo corresponde a cosx negativo e senx positivo. Encontrei exatamente o contrário. Podem me ajudar, por favor?
Obrigada.
-
Lana Brasil
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Dom Abr 07, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Qui Abr 17, 2014 23:32
por e8group » Qui Abr 17, 2014 23:32
A ideia é estabelecer uma conexão entre seno e cosseno . Sabemos que isto é possível , uma das relações que nos permite escreve seno em função de cosseno e vice-versa é relação trigonométrica fundamental :
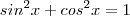
.
Pois bem , vou sugerir uma álgebra que nos leva a resposta
Ps.: O intervalo é

. A função cosseno é sempre negativa neste intervalo ,logo

.
Segue ,
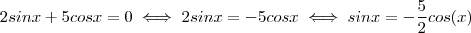
. Podemos dividir ambos membros
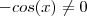
,
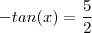
. Como ambos membros é positivo , elevando ao quadrado

. Porém sabemos q

.
Então ,
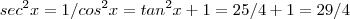
. Logo
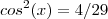
ou seja

. Como

, obtemos
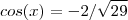
.
Agora tente terminar . Importante é compreender a ideia geral ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Lana Brasil » Sex Abr 18, 2014 14:02
por Lana Brasil » Sex Abr 18, 2014 14:02
santhiago escreveu:A ideia é estabelecer uma conexão entre seno e cosseno . Sabemos que isto é possível , uma das relações que nos permite escreve seno em função de cosseno e vice-versa é relação trigonométrica fundamental :
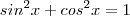
.
Pois bem , vou sugerir uma álgebra que nos leva a resposta
Ps.: O intervalo é

. A função cosseno é sempre negativa neste intervalo ,logo

.
Segue ,
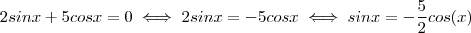
. Podemos dividir ambos membros
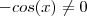
,
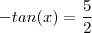
. Como ambos membros é positivo , elevando ao quadrado

. Porém sabemos q

.
Então ,
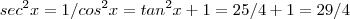
. Logo
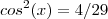
ou seja

. Como

, obtemos
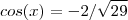
.
Agora tente terminar . Importante é compreender a ideia geral ...
Obrigada pela ajuda.
Eu já havia feito os cálculos e cheguei nos valores de sen x e cos x. O meu problema é só o intervalo. Como cheguei em um valor positivo para o cos x, apenas coloco o sinal negativo? Queria saber por que?
-
Lana Brasil
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Dom Abr 07, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Sex Abr 18, 2014 14:08
por e8group » Sex Abr 18, 2014 14:08
Por favor mostre sua resolução , assim poderei te ajudar. A princípio que posso dizer é q algo errado , cosseno é sempre negativo no intervalo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Lana Brasil » Sex Abr 18, 2014 14:29
por Lana Brasil » Sex Abr 18, 2014 14:29
santhiago escreveu:Por favor mostre sua resolução , assim poderei te ajudar. A princípio que posso dizer é q algo errado , cosseno é sempre negativo no intervalo .
Obrigada novamente. Acabei de descobrir meu erro bobo. Simplesmente esqueci de colocar + e - ao tirar raiz do cos x. Ou seja, a positiva não serve.
-
Lana Brasil
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Dom Abr 07, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Sex Abr 18, 2014 15:30
por e8group » Sex Abr 18, 2014 15:30
Ok. :
Sempre tenha em mente que
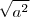
não é

e sim

. Logo , se

,
|a| = - a > 0 , ou seja ,

. Caso , a > 0 ou a = 0 ,
![|a| = a . Neste caso sim [tex] \sqrt{a^2} = a |a| = a . Neste caso sim [tex] \sqrt{a^2} = a](/latexrender/pictures/1a6f2a5ea11181b15f04b0ad004e0aaa.png)
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação trigonométrica] Resolução da equação
por JessicaAraujo » Qui Abr 11, 2013 15:59
- 2 Respostas
- 1722 Exibições
- Última mensagem por JessicaAraujo

Qui Abr 11, 2013 19:12
Funções
-
- Equação Trigonométrica.
por rodsales » Sáb Ago 29, 2009 18:41
- 4 Respostas
- 4037 Exibições
- Última mensagem por rodsales

Sáb Ago 29, 2009 21:19
Trigonometria
-
- equação trigonométrica
por thaa_121 » Qui Abr 08, 2010 15:22
- 1 Respostas
- 3783 Exibições
- Última mensagem por Molina

Qui Abr 08, 2010 23:58
Trigonometria
-
- [Equação Trigonométrica]Equação trigonométrica
por gustavoluiss » Ter Ago 09, 2011 00:32
- 12 Respostas
- 8211 Exibições
- Última mensagem por gustavoluiss

Qua Ago 10, 2011 18:20
Trigonometria
-
- Equação Trigonometrica
por joaofonseca » Seg Nov 28, 2011 00:38
- 5 Respostas
- 2922 Exibições
- Última mensagem por TheoFerraz

Ter Nov 29, 2011 15:53
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


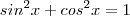 .
.  . A função cosseno é sempre negativa neste intervalo ,logo
. A função cosseno é sempre negativa neste intervalo ,logo  .
. 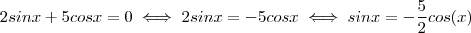 . Podemos dividir ambos membros
. Podemos dividir ambos membros 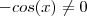 ,
, 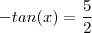 . Como ambos membros é positivo , elevando ao quadrado
. Como ambos membros é positivo , elevando ao quadrado  . Porém sabemos q
. Porém sabemos q  .
.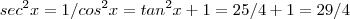 . Logo
. Logo 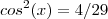 ou seja
ou seja  . Como
. Como  , obtemos
, obtemos 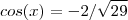 .
.
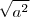 não é
não é  e sim
e sim  . Logo , se
. Logo , se  ,
,  . Caso , a > 0 ou a = 0 ,
. Caso , a > 0 ou a = 0 , ![|a| = a . Neste caso sim [tex] \sqrt{a^2} = a |a| = a . Neste caso sim [tex] \sqrt{a^2} = a](/latexrender/pictures/1a6f2a5ea11181b15f04b0ad004e0aaa.png) .
.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.