-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478076 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 531043 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 494646 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 703617 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2117613 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por thadeu » Qua Nov 18, 2009 13:47
por thadeu » Qua Nov 18, 2009 13:47
Encontre o valor máximo e o valor mínimo que a função
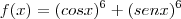
pode assumir
-
thadeu
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Out 19, 2009 14:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Elcioschin » Qua Nov 18, 2009 17:50
por Elcioschin » Qua Nov 18, 2009 17:50
f(x) = (senx)^6 + cos(x)^6
f '(x) = [6*(senx)^5]*cosx + [6*(cosx)^5]*(-senx)
f '(x) = 6*senx*cosx*[(senx)^4 - (cosx)^4]
f '(x) = 3*(2*senx*cosx)*[(sen²x + cos²x)*(sen²x - cos²x)] ----> sen²x + cos²x = 1
f '(x) = 3*sen(2x)*(sen²x - cos²x)
Os pontos de máximo e mínimo da função quando a derivada é nula. Temos portanto:
1) sen(2x) = 0 ----> 2x = 0º ---> x = 0º ----> f(0º) = 1 ----> Valor máximo da função.
2) sen²x - cos²x = 0 ----> sen²x = 1 - sen²x ----> 2*sen²x = 1 ---> sen²x = 1/2 ----> senx = V2/2 -----> x = 45º
f(45º) = (cos45º)^6 + (sen45º)^6 ----> f(45º) = (V2/2)^6 + (V2/2)^6 ----> f(45º) = 1/4 ---> Valor mínimo da função
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Maximo e Minimo]
por Scheu » Sex Mar 16, 2012 01:23
- 1 Respostas
- 2064 Exibições
- Última mensagem por MarceloFantini

Sex Mar 16, 2012 03:14
Cálculo: Limites, Derivadas e Integrais
-
- [Máximo & Minimo]
por allakyhero » Sáb Jun 30, 2012 12:41
- 6 Respostas
- 4296 Exibições
- Última mensagem por allakyhero

Dom Jul 01, 2012 11:06
Cálculo: Limites, Derivadas e Integrais
-
- máximo e minimo
por brunoguim05 » Qua Mai 28, 2014 15:26
- 0 Respostas
- 1303 Exibições
- Última mensagem por brunoguim05

Qua Mai 28, 2014 15:26
Geometria Analítica
-
- Otimização - Máximo e Mínimo
por elbert005 » Dom Jun 05, 2011 20:32
- 0 Respostas
- 4431 Exibições
- Última mensagem por elbert005

Dom Jun 05, 2011 20:32
Cálculo: Limites, Derivadas e Integrais
-
- [Máximo e Mínimo] - Teoria?
por allakyhero » Dom Jul 01, 2012 13:38
- 3 Respostas
- 2084 Exibições
- Última mensagem por e8group

Dom Jul 01, 2012 16:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 13 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
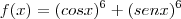 pode assumir
pode assumir

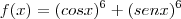 pode assumir
pode assumir


 .
.



