[Trigonometria] Altura da montanha

[jukkax]

Medir alturas de montanhas, em geral, não é simples. Pelo fato de não ser possível obter as medidas do triângulo retângulo teórico que permite o cálculo da altura por meio do uso das relações trigonométricas (a não ser que se fizesse um túnel até o centro da montanha, o que não é prático), deve-se recorrer a outra técnica.



Uma técnica que permite a medição correta da altura é a seguinte: de um ponto no chão, mede-se o ângulo de elevação do chão do topo da montanha (?); caminha-se um valor conhecido de metros para trás (p); mede-se novamente o ângulo de elevação do chão ao topo da montanha (?).

Calcule a altura h de uma montanha sabendo que

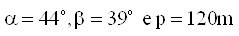
Mod. 8 - QD.2.jpg (2.28 KiB) Exibido 1906 vezes