 por ALPC » Qua Mai 22, 2013 17:50
por ALPC » Qua Mai 22, 2013 17:50
Estou tendo problemas para resolver essa questão de trigonometria no triângulo retângulo no qual eu creio que se pode ser resolvido com Teorema de Pitágoras:

No jogo de bocha, disputado num terreno plano, o objetivo é conseguir lançar uma bola de raio 8 o mais próximo possível de uma bola menor, de raio 4. Num lançamento, um jogador conseguiu fazer com que as duas
bolas ficassem encostadas, conforme ilustra a figura abaixo. A distância entre os pontos A e B, em que as bolas
tocam o chão, é
a) 8
b) 6?2
c) 8?2
d) 4?3
e) 6?3
Resposta: C
Eu tentei resolver da seguinte maneira:



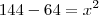

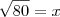
Simplificando:

-

ALPC
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Jan 04, 2013 16:26
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Pedro123 » Qui Mai 23, 2013 16:45
por Pedro123 » Qui Mai 23, 2013 16:45
Seu raciocinio esta 100% correto, porém, na hora de escrever o cateto conhecido, esqueceu de descontar os raios, no caso, nao seria 8, e sim 4 cm. Tente fazer assim. Abraços
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por ALPC » Qui Mai 23, 2013 18:30
por ALPC » Qui Mai 23, 2013 18:30
Oi Pedro, ainda não estou conseguindo entender o motivo daquele cateto medir 4 e não 8.
O exercício diz:
No jogo de bocha, disputado num terreno plano, o objetivo é conseguir lançar uma bola de raio 8 o mais próximo possível de uma bola menor, de raio 4.
Pelo que eu entendi disso, esse cateto que vai do raio da maior bola até o ponto A deve medir 8, pois esse cateto começa do raio(8) até o ponto A.
Você poderia me explicar isso?
-

ALPC
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Jan 04, 2013 16:26
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Pedro123 » Qui Mai 23, 2013 21:51
por Pedro123 » Qui Mai 23, 2013 21:51
Então... Pelo que eu estou vendo, creio que está confundindo onde o triângulo retângulo é formado, tomei a liberdade de usar o desenho acima para ilustrar melhor o que acontece. O fato é, o triângulo retângulo é formado pelos pontos CFD, e não pelos pontos CAB. Porém, como podemos ver, o segmento AB é igual ao segmento DF, portanto basta calcularmos DF para sabermos AB. Veja tambem que o cateto CF não é igual à 8, pois não é CA, sendo assim, ele é uma diferença entre CA (8) e FA, onde FA é igual a BD, que vale 4, pois é o raio da esfera menor. Assim, CF = CA - AF = 8 - 4 = 4
Creio que agora ficou um pouco menos confuso o meu pensamento. Se tiver mais dúvidas, é so falar. abraços
- Anexos
-
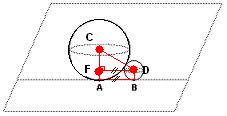
- exer_01.jpg (5.54 KiB) Exibido 7111 vezes
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por ALPC » Dom Mai 26, 2013 00:20
por ALPC » Dom Mai 26, 2013 00:20
Agora eu consegui entender Pedro, obrigado.
-

ALPC
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Jan 04, 2013 16:26
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teorema de Pitágoras - dúvidas no problema
 por Sal » Sáb Mar 24, 2012 20:03
por Sal » Sáb Mar 24, 2012 20:03
- 0 Respostas
- 4742 Exibições
- Última mensagem por Sal

Sáb Mar 24, 2012 20:03
Geometria Plana
-
- teorema de pitagoras
por stanley tiago » Sex Jan 21, 2011 15:59
- 5 Respostas
- 4663 Exibições
- Última mensagem por stanley tiago

Sáb Jan 22, 2011 15:49
Geometria Analítica
-
- teorema de pitagoras
por stanley tiago » Dom Fev 13, 2011 18:35
- 4 Respostas
- 3496 Exibições
- Última mensagem por stanley tiago

Seg Fev 14, 2011 22:00
Geometria Analítica
-
- teorema de pitagoras
por stanley tiago » Sáb Fev 19, 2011 10:26
- 1 Respostas
- 1920 Exibições
- Última mensagem por stanley tiago

Dom Fev 20, 2011 17:48
Geometria Analítica
-
- Teorema de Pitágoras
por Lorrane12 » Sex Mar 23, 2012 19:50
- 9 Respostas
- 12631 Exibições
- Última mensagem por DanielFerreira

Sex Mar 30, 2012 00:19
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




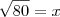





 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
