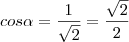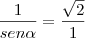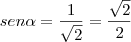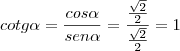por jp_jp300 » Ter Set 25, 2007 18:57
por jp_jp300 » Ter Set 25, 2007 18:57
Meu professor passou estas formulas e estes exercìcios: Alguém sabe resover?
Ele não sabe dar aula e ainda cobra dos alunos!!! Isto vale 7 e é pro dia 28!!! Me ajudem, por favor!!
tg? = sen?/cos?
cotg? = cos?/sen?
sec = 1/cos?
cossec? = 1/sen?
(cos?)² + (sen?)² = 1
a) cos? = -4/5
b) cossec? = 13/5
c) sec? = 2
d)tg? =4/3
e) cotg? = 1
f) cotg? = ?3
Eu não consegui por as frações uma emcima da outra e "?" é aletra grega "alfa"
-
jp_jp300
-
 por jp_jp300 » Ter Set 25, 2007 19:14
por jp_jp300 » Ter Set 25, 2007 19:14
Ah... Esqueci!!! meu professor pediu para dar a resposta de cada questão em cada formula.
-
jp_jp300
-
 por admin » Ter Set 25, 2007 19:34
por admin » Ter Set 25, 2007 19:34
Olá.
Por favor, esclareça o que está sendo perguntado no exercício.
Ou seja, qual é a questão?
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por jp_jp » Qua Set 26, 2007 16:35
por jp_jp » Qua Set 26, 2007 16:35
Não existe pergunta formada.
O professor apenas pasou as formulas, as questões e pediu para que cada questão fosse calculada em cada formula.
-
jp_jp
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Set 25, 2007 18:10
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Qua Set 26, 2007 17:35
por admin » Qua Set 26, 2007 17:35
jp_jp escreveu:Não existe pergunta formada.
O professor apenas pasou as formulas, as questões e pediu para que cada questão fosse calculada em cada formula.
Olá
jp_jp.
Sugiro que solicite ao seu professor esta informação.
Vale para qualquer exercício, você precisa saber o que calcular.
Além disso, seria interessante uma discussão sobre as origens destas chamadas "fórmulas".
Abraço!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por IMEano02 » Qua Set 26, 2007 18:10
por IMEano02 » Qua Set 26, 2007 18:10
jp_jp
De fato a questão está mal formulada, ou talvez EU não tenha entendido o enunciado (se é que ele existe!).
Talvez seu professor tenha solicitado os valores dos ângulos "a" (alfa). Ou, uma vez definidos os conceitos de tangente, secante, cossecante e cotagente, você tenha de escrevê-los apenas em função do seno e do cosseno.
As duas situações acima são apenas hipóteses, ou seja, é necessário o enunciado para podermos te ajudar.
Exemplo: Tendo em vista que estas funções "co" são sempre as inversas de outras funções este exercício não me parece um abuso do seu professor.
Caso vc tenha em mãos um livro de Matemática leia as definições, certamente elas reforçarão as minhas palavras acima.
De qualquer forma, dada a escassez de tempo, encaminho a minha intuição (experiência de ex-aluno do Ensino Médio):
Segue abaixo o meu "palpite" para a sua solução (e quem sabe minha contribuição para uma nota diferente de zero!):
Uma vez que antes dos itens de a) a f) exitem algumas definições, tratemos de utilizá-las:
Portanto teremos:
a) cos? = -4/5, podemos determinar o valor da secante, pois: sec = 1/cos?, donde obtemos que sec = -5/4, ou seja, perceba que o "valor numérico" da secante corresponde ao inverso do valor do cosseno!
Da mesma forma procedemos nos demais itens, ou seja:
b) cossec? = 13/5, aqui temos que o valor numérico da cossecante corresponde ao inverso do valor do seno, ou seja, da relação anteriormente mencionada por vc ( cossec? = 1/sen?) tiramos que: sena = 1/cosseca, sendo assim: sena = 5/13.
c) sec? = 2, semelhante ao que vimos no item a), podemos escrever: uma vez que sec = 1/cos?, temos que: cosa = 1/2.
Você está percebendo a relação que existe entre essas funções?
Como elas se relacionam pelo inverso de cada uma, uma vez que sabemos o valor de uma delas somos "capazes" de obter o valor da outra função, esclarecendo que neste caso as funções em questão são as funções trigonométricas, ou seja: seno, cosseno, tangente, secante, cossecante e cotangente.
Perceba que por se tratar de "funções inversas" para alguns valores numéricos as funções trigonométricas podem não estar definidas, serei mais explícito: quando você se deparar com a situação em que o denominador corresponde ao valor zero caberá uma análise mais cuidadosa, por isso a necessidade de se compreender o SIGNIFICADO destas funções, pois através de seus respectivos gráficos podemos evitar certos erros!
Dando prosseguimento aos outros três itens ainda pendentes:
d) tg? =4/3, daqui podemos obter o valor numérico de duas funções, isto porque: tg? = sen?/cos?, ou seja, sena = 4 e cosa = 3.
e) cotg? = 1, das definições descritas na sua pergunta também temos que: cotg? = cos?/sen?, ou seja, perceba que a cotangente corresponde ao inverso da função tangente, ou seja, cotga = 1/(sena/cosa) = cosa/sena, donde concluímos apenas pela igualdade entre os valores do seno e do cosseno, pois a razão entre eles corresponde a 1.
Aqui no item e) deparamo-nos com uma sutileza, ou seja, como o quociente "cosa/sena" resulta em 1 concluímos pela igualdade mencionada anteriormente, ou seja, cosa = sena.
Só que nas relações fornecidas por você temos que: (cos?)² + (sen?)² = 1, e, substituindo o cosa por sena, obtemos:
(sen?)² + (sen?)² = 1, ou seja, 2(sen?)² = 1, donde: (sen?)² = 1/2, resultando em: sena = ?2/2. (lembre-se que para obter este resultado basta multiplicar a fração obtida por ?2/?2, ou seja, (1/?2) * (?2/?2) = ?2/2, certo?).
Perceba que caso você substituísse o sena por cosa na igualdade acima obteria o mesmo resultado, pois já sabemos que cosa = sena.
E, FINALMENTE:
f) cotg? = ?3, assim como vimos no item anterior temos que: cotg? = cos?/sen?, ou seja, de maneira mais explícita, temos que: cosa = ?3 e que sena = 1, isto porque: cotga = ?3 = ?3/1 = cosa/sena.
Espero ter te ajudado.
E não fique com raiva do professor e muito menos de mim!
Lembre-se de consultar um livro para analisar melhor alguns exemplos.
Certamente esta foi a intenção do seu professor, ou seja, que os alunos percebessem as relações existentes entre as funções trigonométricas.
Repare que no decorrer dos seis itens propostos [do a) ao f)] utilizamos todas as relações mencionadas no enunciado fornecido por você!!
Sugiro que escreva as soluções novamente, utilizando a simbologia adequada, ou seja, exagerei no texto para tentar facilitar a sua compreensão, e espero que você seja mais enxuto, utilizando, por exemplo, o símbolo de "isto implica que", ou seja, a famigerada "flechinha".
Abraço,
E até mais!
-
IMEano02
- Colaborador - Professor

-
- Mensagens: 1
- Registrado em: Qua Set 05, 2007 17:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por admin » Ter Mar 11, 2008 21:28
por admin » Ter Mar 11, 2008 21:28
Olá.
Os itens
(d),
(e) e
(f) precisam de mais cuidado porque o conjunto imagem das funções seno e cosseno é limitado, vejam:
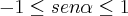

Em outras palavras, não pode ocorrer que:
Podemos obter os valores corretos por Pitágoras e semelhança de triângulos, no círculo trigonométrico:
Em
d) 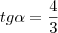
Represente a tangente no círculo trigonométrico, cujo valor é

.
No triângulo retângulo relacionado, a tangente é um cateto. O outro cateto tem valor 1.
Por Pitágoras, encontramos a hipotenusa, cujo valor é

.
Por semelhança de triângulos, encontramos o valor do seno:
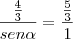


Também por semelhança, encontramos o valor do cosseno:


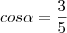
Reparem que os valores de seno e cosseno atendem à condição da imagem (estão entre -1 e 1) e ainda vale a relação inicial:
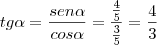
Para o caso
f) 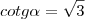
Analogamente, desenhe o triângulo retângulo relacionado à cotangente no círculo trigonométrico.
A cotangente é um dos catetos, o outro vale 1.
Por Pitágoras, encontramos a hipotenusa que vale 2.
E somente então, por semelhança, encontramos o cosseno:

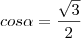
E também o seno:

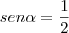
Conferindo a relação inicial:

Em
e) 
Também encontramos a hipotenusa por Pitágoras.
Um cateto é a cotangente que vale 1, o outro também é 1, logo a hipotenusa é

.
Por semelhança, encontramos o cosseno:

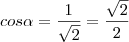
E o seno, idem:
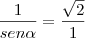
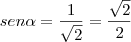
Tanto que:
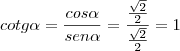
Como sempre deve ocorrer, os valores de seno e cosseno estão entre -1 e 1.
Vale ressaltar também que a "função inversa" do seno é arcsen!
A "função inversa" do cosseno é arccos!
Mais detalhes neste outro tópico:
círculo unitário e algumas relações trigonométricas.
Espero ter ajudado!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcule sen, cos e cotg
por andersontricordiano » Qua Jan 18, 2012 21:44
- 1 Respostas
- 1619 Exibições
- Última mensagem por ant_dii

Qui Jan 19, 2012 01:55
Trigonometria
-
- Derivadas com cotg e cos sen e cos
por Matheus321 » Seg Nov 21, 2016 16:47
- 1 Respostas
- 5080 Exibições
- Última mensagem por Cleyson007

Seg Nov 21, 2016 20:46
Cálculo: Limites, Derivadas e Integrais
-
- geometria
por ehrefundini » Ter Abr 22, 2008 16:53
- 3 Respostas
- 7312 Exibições
- Última mensagem por admin

Qui Mai 01, 2008 15:57
Pedidos de Materiais
-
- geometria 2
por ehrefundini » Qua Mai 07, 2008 10:35
- 1 Respostas
- 6028 Exibições
- Última mensagem por admin

Qua Mai 07, 2008 10:59
Pedidos de Materiais
-
- Geometria
por rybb » Ter Ago 25, 2009 07:48
- 1 Respostas
- 2862 Exibições
- Última mensagem por Elcioschin

Seg Out 05, 2009 22:41
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




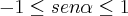

 ou
ou 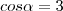 ou
ou 
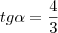
 .
. .
.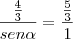




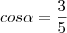
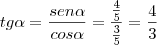
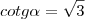

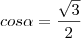

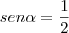


 .
.