 por Churchill » Sex Out 15, 2010 19:27
por Churchill » Sex Out 15, 2010 19:27
Na figura estão representadas, em referencial o.n xOy, uma recta AB e uma circunferência com centro na origem e raio igual a 5. Os pontos A e B pertencem à circunferência. O ponto A também pertence ao eixo das abcissas.
Admita que o ponto B se desloca ao longo da circunferência, no primeiro quadrante.
Para cada posição do ponto B, seja

a amplitude do ângulo orientado cujo lado origem é o semieixo positivo Ox e cujo lado extremidade é a semi-recta OB.

- Seja d o comprimento do segmento de recta [AB], mostre que
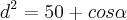
Eu comecei por fazer imaginar um triângulo rectângulo, utilizando o teorema de Pitágoras.
![{d}^{2}= (5+5cos\alpha)^2 + \sqrt[]{(5)^2-(5cos\alpha)^2}^2 {d}^{2}= (5+5cos\alpha)^2 + \sqrt[]{(5)^2-(5cos\alpha)^2}^2](/latexrender/pictures/4a735ccb707db40dbbbb9b10caa6260e.png)
Provavelmente não chego ao resultado ou por estar a errar o cálculo, enganando me no caso notável ou até mesmo por estar a errar o raciocínio. Por esse motivo agradecia que alguém me pudesse ajudar e explicar a forma de chegar ao resultado.
Cumprimentos, Churchill
-
Churchill
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Out 02, 2010 18:52
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Ciências e tecnologias
- Andamento: cursando
 por MarceloFantini » Ter Out 19, 2010 17:23
por MarceloFantini » Ter Out 19, 2010 17:23
Churchill, se for assim:

, então está feito.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida em Trigonometria.
por Rafaeloio3 » Qua Jun 16, 2010 23:16
- 2 Respostas
- 2632 Exibições
- Última mensagem por Rafaeloio3

Qui Jun 17, 2010 14:29
Trigonometria
-
- [trigonometria]DÚVIDA!!
por Flavia R » Qui Set 22, 2011 19:41
- 3 Respostas
- 1575 Exibições
- Última mensagem por MarceloFantini

Qui Set 22, 2011 23:51
Trigonometria
-
- Duvida em trigonometria
por bmachado » Qua Abr 04, 2012 20:56
- 2 Respostas
- 1469 Exibições
- Última mensagem por bmachado

Qui Abr 05, 2012 00:09
Trigonometria
-
- Duvida em trigonometria
por bmachado » Ter Abr 10, 2012 19:04
- 1 Respostas
- 1099 Exibições
- Última mensagem por MarceloFantini

Ter Abr 10, 2012 21:24
Trigonometria
-
- Dúvida em questão de Trigonometria
por carlosvinnicius » Qui Fev 24, 2011 21:00
- 3 Respostas
- 3371 Exibições
- Última mensagem por yanagranhen

Ter Abr 02, 2013 21:09
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 a amplitude do ângulo orientado cujo lado origem é o semieixo positivo Ox e cujo lado extremidade é a semi-recta OB.
a amplitude do ângulo orientado cujo lado origem é o semieixo positivo Ox e cujo lado extremidade é a semi-recta OB.
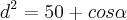
![{d}^{2}= (5+5cos\alpha)^2 + \sqrt[]{(5)^2-(5cos\alpha)^2}^2 {d}^{2}= (5+5cos\alpha)^2 + \sqrt[]{(5)^2-(5cos\alpha)^2}^2](/latexrender/pictures/4a735ccb707db40dbbbb9b10caa6260e.png)


 , então está feito.
, então está feito.
