Admita que o ponto B se desloca ao longo da circunferência, no primeiro quadrante.
Para cada posição do ponto B, seja
a amplitude do ângulo orientado cujo lado origem é o semieixo positivo Ox e cujo lado extremidade é a semi-recta OB.
- Seja d o comprimento do segmento de recta [AB], mostre que
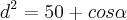
Eu comecei por fazer imaginar um triângulo rectângulo, utilizando o teorema de Pitágoras.
![{d}^{2}= (5+5cos\alpha)^2 + \sqrt[]{(5)^2-(5cos\alpha)^2}^2](/latexrender/pictures/4a735ccb707db40dbbbb9b10caa6260e.png "{d}^{2}= (5+5cos\alpha)^2 + \sqrt[]{(5)^2-(5cos\alpha)^2}^2")
Provavelmente não chego ao resultado ou por estar a errar o cálculo, enganando me no caso notável ou até mesmo por estar a errar o raciocínio. Por esse motivo agradecia que alguém me pudesse ajudar e explicar a forma de chegar ao resultado.
Cumprimentos, Churchill
, então está feito.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.