 por adauto martins » Dom Set 22, 2019 12:47
por adauto martins » Dom Set 22, 2019 12:47
(escola naval-exame de admissao 1938)
verificar que,qualquer que seja

,tem-se:
![arcsen(\sqrt[]{(x/(x+a))}=arctg(\sqrt[]{x/a}) arcsen(\sqrt[]{(x/(x+a))}=arctg(\sqrt[]{x/a})](/latexrender/pictures/e9931fbf4f712c70dbd9b48b96550ba1.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Dom Out 06, 2019 16:46
por adauto martins » Dom Out 06, 2019 16:46
soluçao:
façamos
![y=arcsen(\sqrt[]{x/(x+a)}\Rightarrow seny=\sqrt[]{x/(x+a)} y=arcsen(\sqrt[]{x/(x+a)}\Rightarrow seny=\sqrt[]{x/(x+a)}](/latexrender/pictures/96e8919b8cb2dabf27cd256050485b2f.png)
,temos que:
![{seny}^{2}+{cosy}^{2}=1\Rightarrow cosy=\sqrt[]{1-({seny})^{2}}=\sqrt[]{1-x/(x+a)}=\sqrt[]{a/x+a} {seny}^{2}+{cosy}^{2}=1\Rightarrow cosy=\sqrt[]{1-({seny})^{2}}=\sqrt[]{1-x/(x+a)}=\sqrt[]{a/x+a}](/latexrender/pictures/a0a4ddae6af3fac9f0e5fc65db7ab881.png)
,
logo:
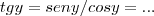
(*) façam os devidos calculos e ...
![y=arctg\sqrt[]{x/a}... y=arctg\sqrt[]{x/a}...](/latexrender/pictures/327acd5a33e697152986d9da905dec3a.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 15:41
- 1 Respostas
- 12331 Exibições
- Última mensagem por DanielFerreira

Ter Set 17, 2019 12:53
Equações
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 15:51
- 1 Respostas
- 12624 Exibições
- Última mensagem por DanielFerreira

Ter Set 17, 2019 12:45
Polinômios
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 16:02
- 1 Respostas
- 4912 Exibições
- Última mensagem por adauto martins

Qui Set 19, 2019 09:39
Equações
-
- exerc.proposto
por adauto martins » Seg Set 16, 2019 16:09
- 4 Respostas
- 8702 Exibições
- Última mensagem por adauto martins

Sex Out 11, 2019 10:34
Números Complexos
-
- exerc.proposto
por adauto martins » Ter Set 17, 2019 10:30
- 1 Respostas
- 4211 Exibições
- Última mensagem por adauto martins

Seg Set 23, 2019 23:57
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ,tem-se:
,tem-se:![arcsen(\sqrt[]{(x/(x+a))}=arctg(\sqrt[]{x/a}) arcsen(\sqrt[]{(x/(x+a))}=arctg(\sqrt[]{x/a})](/latexrender/pictures/e9931fbf4f712c70dbd9b48b96550ba1.png)

 ,tem-se:
,tem-se:![arcsen(\sqrt[]{(x/(x+a))}=arctg(\sqrt[]{x/a}) arcsen(\sqrt[]{(x/(x+a))}=arctg(\sqrt[]{x/a})](/latexrender/pictures/e9931fbf4f712c70dbd9b48b96550ba1.png)

![y=arcsen(\sqrt[]{x/(x+a)}\Rightarrow seny=\sqrt[]{x/(x+a)} y=arcsen(\sqrt[]{x/(x+a)}\Rightarrow seny=\sqrt[]{x/(x+a)}](/latexrender/pictures/96e8919b8cb2dabf27cd256050485b2f.png) ,temos que:
,temos que:![{seny}^{2}+{cosy}^{2}=1\Rightarrow cosy=\sqrt[]{1-({seny})^{2}}=\sqrt[]{1-x/(x+a)}=\sqrt[]{a/x+a} {seny}^{2}+{cosy}^{2}=1\Rightarrow cosy=\sqrt[]{1-({seny})^{2}}=\sqrt[]{1-x/(x+a)}=\sqrt[]{a/x+a}](/latexrender/pictures/a0a4ddae6af3fac9f0e5fc65db7ab881.png) ,
,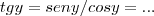
![y=arctg\sqrt[]{x/a}... y=arctg\sqrt[]{x/a}...](/latexrender/pictures/327acd5a33e697152986d9da905dec3a.png)



 , avisa que eu resolvo.
, avisa que eu resolvo.

