 por FilipeMSoares » Sex Mai 24, 2019 19:35
por FilipeMSoares » Sex Mai 24, 2019 19:35
Meu exercício é de faculdade, mas acho que não terá problema, porque não acho que tenha sido a intenção da professora usar matemática de faculdade nessa questão. O problema é o seguinte:
Descreva como resolver o seguinte problema tanto com os métodos tradicionais (lapis, papel, etc) quanto com Geogebra
Construa um triângulo dado lado AB de comprimento c, ângulo ? a partir do vértice A e mediana mB.
O problema pede para você descrever os passos que cumprem a tarefa tanto com o método tradicional (papel, lápis, etc) e tanto com o Geogebra.
No Geogebra, eu preciso deixar o lado que a mediana mB toca com o tamanho correto. Não estou perguntando como fazer isso com o Geogebra: eu quero ajuda em como chegar com uma fórmula que defina o tamanho do lado em função das três variáveis descritas no problema. Eu já tentei utilizar seno e cosseno da soma dos ângulos, lei do seno, lei do cosseno, teorema de pitágoras e a propriedade que a mediana divide o triângulo em duas áreas de tamanho igual. Até agora, sem sucesso. Não sei mais como abordar o problema.
Qualquer dica, ajuda, sermão é bem-vindo.
Por favor, me ajudem.
- Anexos
-
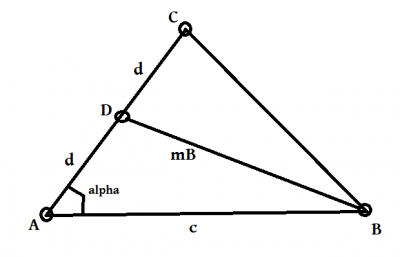
- Uma imagem para uma visualização. Eu preciso obter o d no desenho.
-
FilipeMSoares
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Mai 24, 2019 19:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Manipulação e Cálculo
por Jhenrique » Sex Dez 07, 2012 20:50
- 4 Respostas
- 4779 Exibições
- Última mensagem por Jhenrique

Seg Dez 17, 2012 12:51
Cálculo: Limites, Derivadas e Integrais
-
- [Manipulação de Proporções]
por Tatasacchi_123 » Seg Abr 08, 2013 13:12
- 1 Respostas
- 2488 Exibições
- Última mensagem por DanielFerreira

Seg Abr 08, 2013 17:04
Funções
-
- [Cálculo 1] Manipulação de função
por Larissa28 » Ter Mar 24, 2015 23:54
- 2 Respostas
- 2541 Exibições
- Última mensagem por Larissa28

Qua Mar 25, 2015 19:47
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo 1] Manipulação de função
por Larissa28 » Dom Set 27, 2015 22:24
- 7 Respostas
- 6124 Exibições
- Última mensagem por adauto martins

Qua Set 30, 2015 17:19
Sequências
-
- [ÁLGEBRA EM FÓRMULAS]
por Andreyan » Qui Ago 16, 2012 14:09
- 4 Respostas
- 3040 Exibições
- Última mensagem por Russman

Sex Ago 17, 2012 16:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 .
.



