-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478236 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 532456 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 495965 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 707593 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2124801 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por brunadultra » Qua Jan 23, 2013 15:51
por brunadultra » Qua Jan 23, 2013 15:51
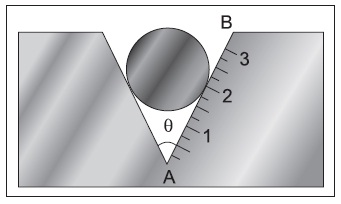
Questão 15 (UNEB 2013): A figura mostra um instrumento utilizado para medir o
diâmetro de pequenos cilindros. Ele consiste em um
bloco metálico que tem uma fenda com o perfil em
forma de V, contendo uma escala. O cilindro é colocado
na fenda e a medida de seu diâmetro, em centímetros,
é o número que, na escala, corresponde ao ponto de
tangência entre o cilindro e o segmento AB.
Nessas condições, ao construir a escala de um
instrumento desses, o número 2 corresponde a um
certo ponto do segmento AB.
Sendo d a distância desse ponto ao ponto A, pode-se afirmar que o valor de d, em cm, é:
Resposta: RAÍZ DE 1+cos(teta)/1-cos(teta)
- Anexos
-
- FIGURA
- mat2.jpg (15.42 KiB) Exibido 9577 vezes
-
brunadultra
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Nov 07, 2012 23:01
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Qui Jan 24, 2013 10:31
por e8group » Qui Jan 24, 2013 10:31
Bom dia .Veja a figura em anexo
Façamos ,
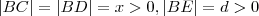
( o que queremos )
Pelo enunciado , obtemos que o raio da circunferência tem medida 1 u.c (Se permancer dúvidas leia novamente o texto ).
No triângulo retângulo , AEC temos que :
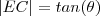
(note que

é agudo por isso desprezamos o módulo )
Ora ,se

então :

(1) .
Por outro lado ,
no triângulo BED , obtemos que
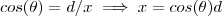
(2)
Comparando as expressões (1) e (2) ,segue que :
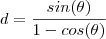
que em consequência da relação trigonométrica fundamental
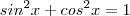
obtemos ,
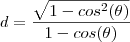
que devido a propriedade
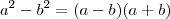
e por multiplicarmos tanto o numerador quanto denominador por

,finalmente obtemos :
d= \frac{ \sqrt{ 1 + cos(\theta)} }{ \sqrt{ 1 - cos(\theta)}
OBS.: Aconselho que refaça todas as contas , pois foi omitido algumas contas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por brunadultra » Qui Jan 24, 2013 13:47
por brunadultra » Qui Jan 24, 2013 13:47
Olá santhiago,
eu consegui chegar até a parte em que
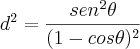
. A partir daí eu encontro um resultado que não bate com a resposta:
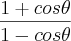
(dentro da raíz)
Você poderia me ajudar?
-
brunadultra
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Nov 07, 2012 23:01
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Qui Jan 24, 2013 21:02
por e8group » Qui Jan 24, 2013 21:02
Boa noite . Começando de onde você chegou(que estar correto) , podemos comparar o numerador
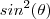
com a indentidade trigonométrica fundamental
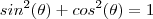
de onde vamos obter
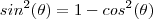
. Ou seja ,
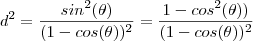
.Extraindo a raiz quadrada de ambos membros ,
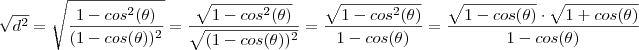
. E por fim , multiplicando-se

por
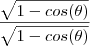
(note que não estamos alterando o resultado ,estamos multiplicando por 1 que é o elemento neutro do produto ) ,
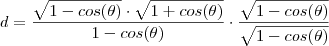
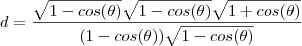
![d= \frac{\sqrt{[1-cos(\theta)]^2} \sqrt{1+cos(\theta)}}{(1-cos(\theta))\sqrt{1-cos(\theta)}} d= \frac{\sqrt{[1-cos(\theta)]^2} \sqrt{1+cos(\theta)}}{(1-cos(\theta))\sqrt{1-cos(\theta)}}](/latexrender/pictures/ea0e49739f2324454506473f9564bb3f.png)
![d= \frac{[1-cos(\theta)]\sqrt{1+cos(\theta)}}{(1-cos(\theta))\sqrt{1-cos(\theta)}} d= \frac{[1-cos(\theta)]\sqrt{1+cos(\theta)}}{(1-cos(\theta))\sqrt{1-cos(\theta)}}](/latexrender/pictures/3e7b3f100b16f319b4970d021e5a1c5c.png)
Após cancelarmos o termo

" encima e embaixo "

Qualquer dúvida só postar .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Sex Jan 25, 2013 08:17
por e8group » Sex Jan 25, 2013 08:17
Ou melhor ...


.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por zenildo » Qua Dez 13, 2017 17:28
por zenildo » Qua Dez 13, 2017 17:28
Eu não entendi o porquê de colocar BC, já que tinha B naquele ponto.Tambem não entendi o porquê de BC = BD e escrever que é igual a x. Por favor, me explique.
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [POLINÔMIOS] Questão UNEB 2013
 por brunadultra » Qua Jan 23, 2013 13:58
por brunadultra » Qua Jan 23, 2013 13:58
- 4 Respostas
- 4429 Exibições
- Última mensagem por young_jedi

Sáb Set 07, 2013 19:04
Polinômios
-
- [Função] Questão UNEB 2013
por brunadultra » Qua Jan 23, 2013 16:15
- 1 Respostas
- 8934 Exibições
- Última mensagem por young_jedi

Qui Jan 24, 2013 21:54
Funções
-
- [LOGARITMO] QUESTÃO UNEB 2013
por brunadultra » Qua Jan 23, 2013 18:17
- 2 Respostas
- 5959 Exibições
- Última mensagem por brunadultra

Qua Jan 23, 2013 20:47
Logaritmos
-
- [PROBABILIDADE] Questão UNEB 2013
 por brunadultra » Qua Jan 23, 2013 22:05
por brunadultra » Qua Jan 23, 2013 22:05
- 2 Respostas
- 5909 Exibições
- Última mensagem por Julliana_Ferrari

Qua Mar 02, 2016 01:32
Probabilidade
-
- QUESTÃO de Progressão Aritimética UNEB 2013
 por jessicaaangels » Sáb Set 28, 2013 11:59
por jessicaaangels » Sáb Set 28, 2013 11:59
- 2 Respostas
- 4590 Exibições
- Última mensagem por Thiago 86

Sex Out 11, 2013 12:27
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 24 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


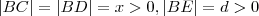 ( o que queremos )
( o que queremos ) 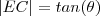 (note que
(note que  é agudo por isso desprezamos o módulo )
é agudo por isso desprezamos o módulo ) então :
então :  (1) .
(1) .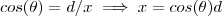 (2)
(2) 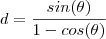 que em consequência da relação trigonométrica fundamental
que em consequência da relação trigonométrica fundamental 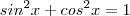 obtemos ,
obtemos , 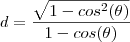 que devido a propriedade
que devido a propriedade 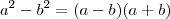 e por multiplicarmos tanto o numerador quanto denominador por
e por multiplicarmos tanto o numerador quanto denominador por  ,finalmente obtemos :
,finalmente obtemos : 
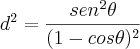 . A partir daí eu encontro um resultado que não bate com a resposta:
. A partir daí eu encontro um resultado que não bate com a resposta: 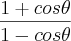 (dentro da raíz)
(dentro da raíz) 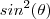 com a indentidade trigonométrica fundamental
com a indentidade trigonométrica fundamental 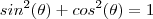 de onde vamos obter
de onde vamos obter 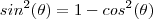 . Ou seja ,
. Ou seja , 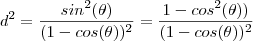 .Extraindo a raiz quadrada de ambos membros ,
.Extraindo a raiz quadrada de ambos membros , 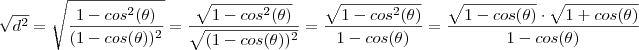 . E por fim , multiplicando-se
. E por fim , multiplicando-se  por
por 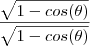 (note que não estamos alterando o resultado ,estamos multiplicando por 1 que é o elemento neutro do produto ) ,
(note que não estamos alterando o resultado ,estamos multiplicando por 1 que é o elemento neutro do produto ) ,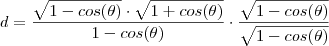
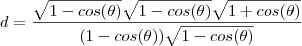
![d= \frac{\sqrt{[1-cos(\theta)]^2} \sqrt{1+cos(\theta)}}{(1-cos(\theta))\sqrt{1-cos(\theta)}} d= \frac{\sqrt{[1-cos(\theta)]^2} \sqrt{1+cos(\theta)}}{(1-cos(\theta))\sqrt{1-cos(\theta)}}](/latexrender/pictures/ea0e49739f2324454506473f9564bb3f.png)
![d= \frac{[1-cos(\theta)]\sqrt{1+cos(\theta)}}{(1-cos(\theta))\sqrt{1-cos(\theta)}} d= \frac{[1-cos(\theta)]\sqrt{1+cos(\theta)}}{(1-cos(\theta))\sqrt{1-cos(\theta)}}](/latexrender/pictures/3e7b3f100b16f319b4970d021e5a1c5c.png)
 " encima e embaixo "
" encima e embaixo " 

 .
.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.