[Dedução do Período do Pêndulo Simples]

[Guga1981]

Olá amigos!
Primeiramente parabéns pelo fórum! É um dos melhores da internet! Tanto que escolhi aqui para postar este questionamento.
Vamos lá...
Estudando pêndulo simples, cheguei ao entendimento que:
Sendo ? a abertura do Pêndulo Simples, nas extremidades do movimento (e, independente do valor de ?) a resultante é P.sen?, pois nas extremidades a
força tensora (T) se anula com P.cos?, sobrando apenas P.sen?.

Por que razão e por qual motivo eu preciso considerar ? com pequenos ângulos se eu já tenho o valor da força resultante do pêndulo simples
(P.sen?) e o deslocamento percorrido (o deslocamento que no caso é o comprimento L do fio do pêndulo vezes o ângulo ? em radianos (x = L.?). Pois aprendi que, numa secção circular de raio L e borda X, ).
Tendo a força resultante e o deslocamento, posso muito bem relacionar estes valores com a fórmula de força resultante do sistema massa mola que diz:

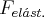= -k.x

(Onde k é a constante elástica e x é o deslocamento percorrido)

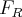= -k.x

No lugar de FR, eu coloco P.sen?

(que é a força resultante do pêndulo simples)

No lugar de x, eu coloco L.?

(que é o deslocamento percorrido pelo pêndulo simples)

E assim tenho:
P.sen? = -k.-L.?
(descolcamento negativo (-L.?) porque deslocamento e força resultante tem sentidos opostos)

m.g.sen? = k.L.?
k =

Agora que eu já tenho a constante k do pêndulo simples, é só substituir na fórmula do período do sistema massa mola que diz:

T= 2?.

T= 2?.

T= 2?.

T= 2?.
E assim eu tenho o período do pêndulo simples para qualquer abertura ?! Estou errado?

Criei uma planilha (link abaixo) demonstrando que a fórmula é coerente com pequenos ângulos (ângulos até 10º) e com todos os outros possíveis:
https://drive.google.com/file/d/19e1oGc ... sp=sharing