por annelopes » Sáb Nov 22, 2014 17:00
Oi gente, não consigo achar o gabarito dessa questão em lugar algum e como ela faz parte de uma lista de exercícios para um trabalho estou desesperada por ajuda, então se alguém puder me ajudar. Obrigada!
- Anexos
-
-
annelopes
- Novo Usuário
-
- Mensagens: 1
- Registrado em: Sáb Nov 22, 2014 16:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo com CDB, e outro com capitalização. Help!!!
por lisaflach » Ter Abr 12, 2011 17:10
- 0 Respostas
- 1284 Exibições
- Última mensagem por lisaflach
Ter Abr 12, 2011 17:10
Matemática Financeira
-
- medida da base do triângulo isósceles
por zenildo » Seg Dez 12, 2016 18:09
- 1 Respostas
- 1536 Exibições
- Última mensagem por petras
Qua Jan 04, 2017 14:23
Geometria Plana
-
- [Geometria espacial] Prisma de base um triângulo equilátero
por rochadapesada » Seg Abr 08, 2013 18:13
- 1 Respostas
- 2753 Exibições
- Última mensagem por aleph
Ter Out 06, 2015 20:31
Geometria Espacial
-
- Bissetriz do ângulo externo oposto
por Balanar » Dom Set 19, 2010 03:57
- 0 Respostas
- 1214 Exibições
- Última mensagem por Balanar
Dom Set 19, 2010 03:57
Geometria Plana
-
- [Lógica Digital] Sistema Numérico Conversão Base X - Base 10
por Luc4sPaulo » Sex Fev 17, 2017 12:32
- 0 Respostas
- 3934 Exibições
- Última mensagem por Luc4sPaulo
Sex Fev 17, 2017 12:32
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.
Em
substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.
2)Na equação
não existem zeros.Senão vejamos
Completando o quadrado,
As coordenadas do vertice da parabola são
O eixo de simetria é a reta
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
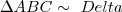DBC \Rightarrow tg60=(h/x)e tg30=(h/50+x)[/tex]...logo ![tg60=(\sqrt[]{3})=(h/3x)\Rightarrow tg30=(\sqrt[]{3}/3)=(h/50+x)\Rightarrow (h/3x)=(h/50+x)\Rightarrow 3x=50+x\Rightarrow x=25...](/latexrender/pictures/05b34b8109cf7706b6f2ec47a76ff1e1.png "tg60=(\sqrt[]{3})=(h/3x)\Rightarrow tg30=(\sqrt[]{3}/3)=(h/50+x)\Rightarrow (h/3x)=(h/50+x)\Rightarrow 3x=50+x\Rightarrow x=25...")
...![h=tg60.x=\sqrt[]{3}.25\Rightarrow h=\sqrt[]{3}.25](/latexrender/pictures/601211951d37a539a350b4b06647f590.png "h=tg60.x=\sqrt[]{3}.25\Rightarrow h=\sqrt[]{3}.25")
