o período e imagem desta função real definida por f(x)=3sen2x é:
Desenvolvi desta forma, mas não bate com as alternativas, devo ter feito algo errado na tabela:
y=f(x)= 3sen2x, vou igualar 2x a um angulo t.
TABELA:
x=t/2 t=2x y=3sent=3sen2x
0 0 0
pi/4 pi/2 1
pi/2 pi 0
3pi/4 3pi/2 -1
pi 2pi 0
período: p=pi-0=pi
Im(f)=[-1,1]
as alternativas que tenho:
a) pi e [-3,3] c)2pi/3 e [-2,2] e)2pi e [-1,1]
b)4pi e [-3,3] d)6pi e [-2,2]


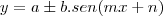 temos que o período e a imagem é dado por:
temos que o período e a imagem é dado por:
![I_m=[a-|b|,a+|b|] I_m=[a-|b|,a+|b|]](/latexrender/pictures/2e3ed0f84128e1e6b60980b22ad4e982.png)
 , onde
, onde  ,
,  ,
, 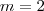 e
e 
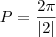

![I_m=[0-|3|,0+|3|] I_m=[0-|3|,0+|3|]](/latexrender/pictures/f7e231f766623c067dde7414bbc2e473.png)
![I_m=[-3,3] I_m=[-3,3]](/latexrender/pictures/f24a01f72680b352c47970d9dce4c25c.png)


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)