Olá!
O que pode estar dificultando é a falta de números, isto é, a resposta será dada em função de "letras" mesmo. Bem, neste exercício, podemos usar as funções da trigonometria. Assim:
Primeiro, precisamos notar que os triângulos ABD e ABC apresentam o lado AB em comum, o que já é um boa "ferramenta". Daí, se aplicarmos TANGENTE para os ângulos

e

, teremos:
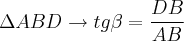
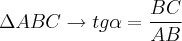
Agora, notemos que

.
Assim, se fizermos
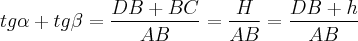
.
A partir deste ponto, podemos obter várias respostas, dependendo de quais são as variáveis as quais a resposta deve estar em função. Neste exercício, parece que a resposta deve estar em função de
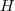
,

,

,

e
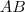
, pois estes foram dados. Então, podemos escrever:

Bem, note que

não está explicitamente na resposta, mas talvez fazendo algumas manipulações algébricas o teríamos. Contudo, não necessariamente todos os elementos dados estão de forma explicita na resposta. Em todo caso, espero que esta seja a resposta correta; você a tem ?
Bom, espero que tenha ajudado. Mesmo que a resposta não esteja desta forma, acho que o raciocínio deve ajudar um pouco.



 e
e  , teremos:
, teremos: 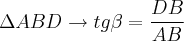
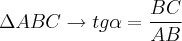
 .
.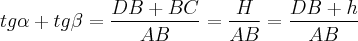 .
.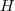 ,
,  ,
, 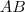 , pois estes foram dados. Então, podemos escrever:
, pois estes foram dados. Então, podemos escrever:



 .
.
 :
: