 por Victor985 » Ter Nov 19, 2013 08:38
por Victor985 » Ter Nov 19, 2013 08:38
(Mauá-SP) Para obter a altura H de uma chaminé, um engenheiro, com um aparelho especial, estabeleceu a horizontal AB e mediu os ângulos ? e ?, tendo a seguir medido BC = h. Determine a altura da chaminé.
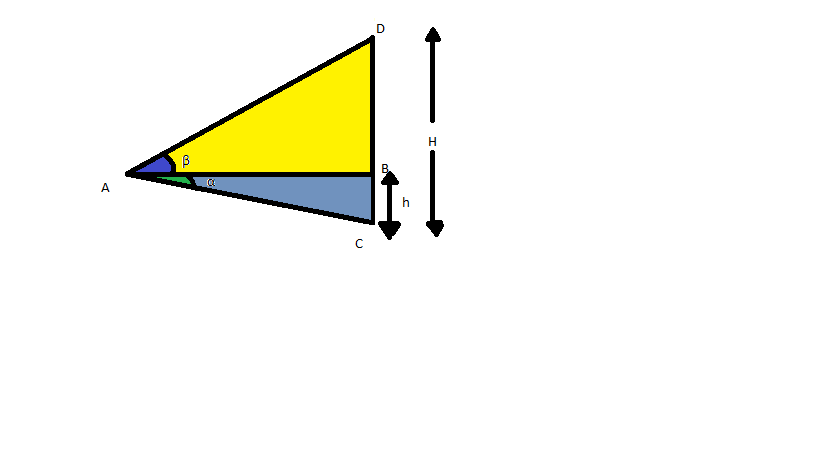
- Triângulo.png (11.43 KiB) Exibido 3884 vezes
Nessa questão, li o enunciado várias vezes, mas infelizmente eu não sei nem como começar a resolvê-la.
-
Victor985
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sáb Nov 02, 2013 12:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Pessoa Estranha » Ter Nov 19, 2013 17:26
por Pessoa Estranha » Ter Nov 19, 2013 17:26
Olá!
O que pode estar dificultando é a falta de números, isto é, a resposta será dada em função de "letras" mesmo. Bem, neste exercício, podemos usar as funções da trigonometria. Assim:
Primeiro, precisamos notar que os triângulos ABD e ABC apresentam o lado AB em comum, o que já é um boa "ferramenta". Daí, se aplicarmos TANGENTE para os ângulos

e

, teremos:
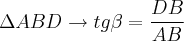
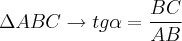
Agora, notemos que

.
Assim, se fizermos
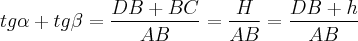
.
A partir deste ponto, podemos obter várias respostas, dependendo de quais são as variáveis as quais a resposta deve estar em função. Neste exercício, parece que a resposta deve estar em função de
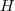
,

,

,

e
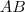
, pois estes foram dados. Então, podemos escrever:

Bem, note que

não está explicitamente na resposta, mas talvez fazendo algumas manipulações algébricas o teríamos. Contudo, não necessariamente todos os elementos dados estão de forma explicita na resposta. Em todo caso, espero que esta seja a resposta correta; você a tem ?
Bom, espero que tenha ajudado. Mesmo que a resposta não esteja desta forma, acho que o raciocínio deve ajudar um pouco.

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Pessoa Estranha » Ter Nov 19, 2013 17:29
por Pessoa Estranha » Ter Nov 19, 2013 17:29
OBS.: Usei tangente, pois estou considerando que trata-se de triângulos retângulos.
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
por anneliesero » Qui Set 13, 2012 18:03
- 4 Respostas
- 3296 Exibições
- Última mensagem por Cleyson007

Sex Set 14, 2012 09:36
Trigonometria
-
- TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
por anneliesero » Ter Set 18, 2012 16:54
- 1 Respostas
- 3182 Exibições
- Última mensagem por Cleyson007

Ter Set 18, 2012 17:42
Trigonometria
-
- RE: TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
por anneliesero » Ter Set 18, 2012 17:08
- 2 Respostas
- 6782 Exibições
- Última mensagem por Cleyson007

Ter Set 18, 2012 17:31
Trigonometria
-
- [Trigonometria] triângulo retângulo e isocéles
por JoseEduardo » Dom Out 09, 2011 03:25
- 2 Respostas
- 1749 Exibições
- Última mensagem por JoseEduardo

Sex Nov 04, 2011 00:44
Trigonometria
-
- [Problema]Trigonometria no Triângulo Retângulo
por ALPC » Ter Jun 18, 2013 17:31
- 0 Respostas
- 1030 Exibições
- Última mensagem por ALPC

Ter Jun 18, 2013 17:31
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 e
e  , teremos:
, teremos: 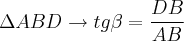
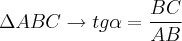
 .
.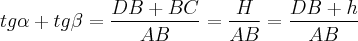 .
.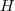 ,
,  ,
, 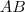 , pois estes foram dados. Então, podemos escrever:
, pois estes foram dados. Então, podemos escrever:




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.