No jogo de bocha, disputado num terreno plano, o objetivo é conseguir lançar uma bola de raio 8 o mais próximo possível de uma bola menor, de raio 4. Num lançamento, um jogador conseguiu fazer com que as duas
bolas ficassem encostadas, conforme ilustra a figura abaixo. A distância entre os pontos A e B, em que as bolas
tocam o chão, é
a) 8
b) 6?2
c) 8?2
d) 4?3
e) 6?3
Resposta: C
Eu tentei resolver da seguinte maneira:



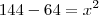

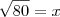
Simplificando:






 .
.
 :
: