 por Gir » Qui Nov 05, 2009 18:11
por Gir » Qui Nov 05, 2009 18:11
Se "theta" é um angulo do 4º quadrante e cotg"theta"=-2/5,qnto vale sen2"theta" - cos2"theta" ?
-2/5=cos"theta"/sen"theta" =>-2/5=1/tg"theta" =>tg"theta"=-5/2
.
.
.
sen2"theta"-cos2"theta"=2"theta"(sen-cos)
.
.
.
cotg²"theta"+1=cossec²"theta"
cossec²"theta"=7/5
me ajudem!essas foram minhas tentativas!!
-
Gir
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jul 02, 2009 17:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Sex Nov 06, 2009 13:34
por Molina » Sex Nov 06, 2009 13:34
Bom dia!

é o que queremos descobrir.
Abrindo esta expressão, temos:
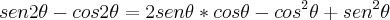
Ficando apenas em função de seno e cosseno.
O único dado que nos é fornecido é que
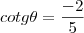

Sugestão: Utilize a fórmula
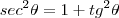
e com isso descubra quanto que vale o

. Posteriormente é fácil descobrir o

.
Qualquer dúvida me informe,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Gir » Sáb Nov 07, 2009 00:18
por Gir » Sáb Nov 07, 2009 00:18
hum...ok...aí fiz assim:
cotg"theta"=1/tg"theta" -> tg"theta"=-5/2
sec²"theta"=1+tg²"theta"
(1/cos"theta")²=1+(-5/2)²
.
.
.
cos²"theta"=4/29 e cos"theta"=2/raiz de 29
substituindo:
2.sen"theta".2 raiz de 29/29 - 4/29 + sen²"theta"
.
.
.
2.sen"theta".sen²"theta".2(raiz de 29 - 2)/29
e agora?
-
Gir
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jul 02, 2009 17:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Sáb Nov 07, 2009 12:29
por Molina » Sáb Nov 07, 2009 12:29
É isso aí.
Agora sabendo

é fácil descobrir quando vale

pela fórmula:
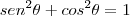
Certo?
Só um detalhe que pode ser necessário fazer para a resposta final dar igual ao do gabarito:
Quando você achou
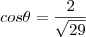
eu sugiro que você racionalize isso:
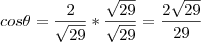
Qualquer dúvida informa aí,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Gir » Sáb Nov 07, 2009 17:10
por Gir » Sáb Nov 07, 2009 17:10
agora estah ficando facil ... ^^
entao,sen²"theta"+cos²"theta"=1 sendo cos²"theta"=4/29
sen²"theta"+4/29=1
.
.
.
sen²"theta"=25/29
logo sen"theta"=5 raiz de 29/29[/]
agora substituindo esses valores na expressao dada
2.5 raiz de 29/29.25/29.2 raiz de 29 - 4/29
.
.
.
250 raiz de 29/841.2 raiz de 29 - 4/29
500.29-4/841.29
cancela 29 c/ 29
e xeguei no resultado=[b]496/841
ta certo?como simplifico?
-
Gir
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jul 02, 2009 17:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Gir » Sex Jan 08, 2010 16:48
por Gir » Sex Jan 08, 2010 16:48
por favor me respondam!

-
Gir
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jul 02, 2009 17:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Sex Jan 08, 2010 19:46
por Molina » Sex Jan 08, 2010 19:46
Gir escreveu:e xeguei no resultado=496/841
ta certo?como simplifico?
Tem que ver se 496 e 841 tem multiplos em comum. Então, pra ficar mais fácil você terá que fatorá-los (encrevendo-os na forma de multiplicação).
Ex: 32 pode ser escrito na forma de
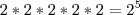
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Gir » Seg Jan 11, 2010 09:37
por Gir » Seg Jan 11, 2010 09:37
entao.fatorando 496 encontrei 2.2.2.2.31 e nao consegui fatorar 841. =/
???
-
Gir
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jul 02, 2009 17:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Seg Jan 11, 2010 10:18
por MarceloFantini » Seg Jan 11, 2010 10:18
Bom dia!

(fui tentando com vários).
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [trigonometria] trigonometria em triangulo qualquer
por biamassa00 » Sex Mai 25, 2012 22:19
- 0 Respostas
- 3597 Exibições
- Última mensagem por biamassa00

Sex Mai 25, 2012 22:19
Trigonometria
-
- (Trigonometria) problema trigonometria
por Luizap11 » Qui Dez 05, 2013 00:33
- 2 Respostas
- 5275 Exibições
- Última mensagem por Edunclec

Qui Dez 05, 2013 20:53
Trigonometria
-
- trigonometria
por Cleyson007 » Qua Set 24, 2008 19:44
- 2 Respostas
- 3416 Exibições
- Última mensagem por admin

Ter Set 30, 2008 19:08
Trigonometria
-
- trigonometria
por Micheline » Dom Jan 25, 2009 16:21
- 5 Respostas
- 4967 Exibições
- Última mensagem por Cleyson007

Seg Jan 26, 2009 17:27
Trigonometria
-
- Trigonometria
por Flavio » Sex Fev 13, 2009 21:29
- 5 Respostas
- 5129 Exibições
- Última mensagem por Molina

Seg Fev 16, 2009 01:53
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 é o que queremos descobrir.
é o que queremos descobrir.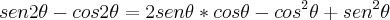
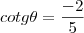
 Sugestão: Utilize a fórmula
Sugestão: Utilize a fórmula 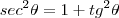 e com isso descubra quanto que vale o
e com isso descubra quanto que vale o  . Posteriormente é fácil descobrir o
. Posteriormente é fácil descobrir o  .
.

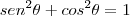
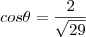 eu sugiro que você racionalize isso:
eu sugiro que você racionalize isso:

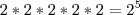
 (fui tentando com vários).
(fui tentando com vários).
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.