por rybb » Ter Ago 25, 2009 00:48
Açguém por favor pode me ajudar com esse exercício??
- Um trapézio isósceles MNQP tem os seguintes dados:
MN = 20 cm, QP = 10 cm e ângulo 60°; calcular a área desse trapézio, em cm².
trapézio:
http://s927.photobucket.com/albums/ad11 ... rapzio.jpg
-
rybb
- Novo Usuário
-
- Mensagens: 3
- Registrado em: Ter Ago 25, 2009 00:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
por Lucio Carvalho » Ter Ago 25, 2009 06:57
Olá rybb,
Tentarei explicar uma das possíveis maneiras de resolver.
De acordo com o exercício, construí a imagem em anexo.
Sabemos que para calcular a área do trapézio, podemos utilizar a seguinte fórmula:
Já conhecemos a base maior e a base menor: bM = 20 cm e bm = 10 cm
Falta-nos a altura (h) que podemos calcular assim:
Então:
![h=5.tg60º=5.\sqrt[]{3}](/latexrender/pictures/54d0b3786ea9bd3d3f64ede680ee56c8.png "h=5.tg60º=5.\sqrt[]{3}")
E, finalmente, calculamos a área:
![A=\left(\frac{20+10}{2} \right).5.\sqrt[]{3}=75.\sqrt[]{3}{cm}^{2}](/latexrender/pictures/9918bbd5d4bc8e5e8a89836b004bb8cd.png "A=\left(\frac{20+10}{2} \right).5.\sqrt[]{3}=75.\sqrt[]{3}{cm}^{2}")
Espero ter ajudado e aguardo a opinião de outros participantes!
- Anexos
-
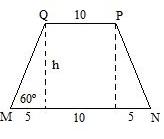
- Trapézio isósceles do exercício.jpg (3.92 KiB) Exibido 2528 vezes
-
Lucio Carvalho
- Colaborador Voluntário
-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [trigonometria] trigonometria em triangulo qualquer
por biamassa00 » Sex Mai 25, 2012 22:19
- 0 Respostas
- 3502 Exibições
- Última mensagem por biamassa00
Sex Mai 25, 2012 22:19
Trigonometria
-
- (Trigonometria) problema trigonometria
por Luizap11 » Qui Dez 05, 2013 00:33
- 2 Respostas
- 5113 Exibições
- Última mensagem por Edunclec
Qui Dez 05, 2013 20:53
Trigonometria
-
- trigonometria
por Cleyson007 » Qua Set 24, 2008 19:44
- 2 Respostas
- 3334 Exibições
- Última mensagem por admin
Ter Set 30, 2008 19:08
Trigonometria
-
- trigonometria
por Micheline » Dom Jan 25, 2009 16:21
- 5 Respostas
- 4843 Exibições
- Última mensagem por Cleyson007
Seg Jan 26, 2009 17:27
Trigonometria
-
- Trigonometria
por Flavio » Sex Fev 13, 2009 21:29
- 5 Respostas
- 4977 Exibições
- Última mensagem por Molina
Seg Fev 16, 2009 01:53
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:
Então pense o seguinte: a fração geratriz de 0,05 é
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
