 por Giudav » Ter Jun 05, 2012 22:03
por Giudav » Ter Jun 05, 2012 22:03
Se tg

=3 e 0<x<90*,então o valor de cos

é:
Minha resolução tg é iqual a sen/cos logo:
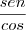
=

Obs:elevei tudo ao quadrado

.

=

.9
1=Sen-1.9
Sen-8
Gabarito:
![\sqrt[]{10}/10 \sqrt[]{10}/10](/latexrender/pictures/4d88a59713a246b39b88e1ddae51fba8.png)
Agradeço desde já
-
Giudav
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Ter Fev 21, 2012 23:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qua Jun 06, 2012 02:32
por MarceloFantini » Qua Jun 06, 2012 02:32
Sua resolução está incorreta, pois seno é uma função limitada nos números reais. Vejamos: temos que

e que

. O intervalo de

nos assegura que cosseno é positivo. Voltando à definição de tangente, temos

.
Vamos agora usar a relação fundamental:

e finalmente

, pois cosseno é positivo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Pre-Universitario) Se seno=10/15 calcule a tangente
por Pre-Universitario » Qui Ago 18, 2011 18:27
- 2 Respostas
- 1675 Exibições
- Última mensagem por Pre-Universitario

Qui Ago 18, 2011 22:45
Trigonometria
-
- Dúvida em valores de seno, cosseno e tangente.
 por Sobreira » Ter Abr 30, 2013 00:40
por Sobreira » Ter Abr 30, 2013 00:40
- 1 Respostas
- 1385 Exibições
- Última mensagem por young_jedi

Ter Abr 30, 2013 12:52
Trigonometria
-
- [Limite trigonométrico] Razão entre tangente e seno.
por Matheus Lacombe O » Dom Out 28, 2012 17:13
- 3 Respostas
- 2507 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 21:53
Cálculo: Limites, Derivadas e Integrais
-
- Seno,cosseno,secante, tangente, contangente,conssecante
por leticiapires52 » Seg Ago 11, 2014 14:59
- 4 Respostas
- 2605 Exibições
- Última mensagem por leticiapires52

Ter Ago 19, 2014 13:46
Trigonometria
-
- Ajuda sobre Limites seno e exponencial
por gn66 » Sex Jun 03, 2011 12:02
- 8 Respostas
- 5078 Exibições
- Última mensagem por gn66

Sex Jun 03, 2011 16:34
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 =3 e 0<x<90*,então o valor de cos
=3 e 0<x<90*,então o valor de cos  é:
é: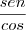 =
=
 .
. =
= .9
.9![\sqrt[]{10}/10 \sqrt[]{10}/10](/latexrender/pictures/4d88a59713a246b39b88e1ddae51fba8.png)

 =3 e 0<x<90*,então o valor de cos
=3 e 0<x<90*,então o valor de cos  é:
é: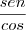 =
=
 .
. =
= .9
.9![\sqrt[]{10}/10 \sqrt[]{10}/10](/latexrender/pictures/4d88a59713a246b39b88e1ddae51fba8.png)

 e que
e que  . O intervalo de
. O intervalo de  nos assegura que cosseno é positivo. Voltando à definição de tangente, temos
nos assegura que cosseno é positivo. Voltando à definição de tangente, temos .
.
 , pois cosseno é positivo.
, pois cosseno é positivo.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
