Bom dia, Ananda!
Neste caso, eu concordo com o livro. Vamos discutir o motivo:
Deixando de lado a equação inicial do problema, se partíssemos apenas daqui:
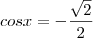
, você estaria certa, pois, de fato, no intervalo

,

deveria ser sim
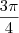
.
O erro está nesta passagem:
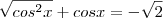

O quadrado de um número (positivo ou negativo), sempre é positivo.
Então, a raiz quadrada de um número ao quadrado, exige um cuidado adicional: o módulo.
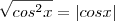
Ananda, reveja o conceito de módulo, é simples mas não menos importante:
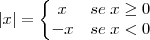
Quando

, o sinal é indiferente, portanto, também pode ser assim:
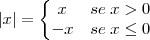
Comentando o significado:
O módulo é a distância até a origem, por isso, seu "serviço" é obter sempre um número positivo.
O condicional "se", trata os dois casos.
i) se o número já é positivo (ou zero), mantenha o mesmo número;
ii) se o número é negativo (ou zero), multiplique por -1, assim, ficará positivo (ou zero).
O problema ao escrever
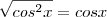
é que apenas um caso é considerado:
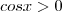
.
E este, o intervalo do enunciado não permite.
Para resumir, sempre que você se deparar com uma raiz de índice par, cujo radicando possui expoente também par, cuidado com esta simplificação direta, utilize módulo.
Continuando daqui:
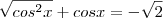

Caso 1) se
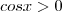
Não ocorre no intervalo

.
Caso 2) se



Também, não ocorre.
Logo, a equação realmente não admite solução no intervalo

.
Adicionalmente, após rever módulo, sugiro que você aproveite e estude novamente alguma teoria sobre números complexos.
Comente caso alguma nova dúvida tenha surgido.
Espero ter ajudado!
Bons estudos!
 , a equação
, a equação![\sqrt[]{1 - {sen}^{2}x} + cosx = - \sqrt[]{2} \sqrt[]{1 - {sen}^{2}x} + cosx = - \sqrt[]{2}](/latexrender/pictures/66cfc5cfae955058fcc408c85cf522ee.png)
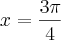
![\sqrt[]{{cos}^{2}x} + cosx = - \sqrt[]{2} \sqrt[]{{cos}^{2}x} + cosx = - \sqrt[]{2}](/latexrender/pictures/bda803f69f0e6db205a9a85df14f5f44.png)
![cosx + cosx = - \sqrt[]{2} cosx + cosx = - \sqrt[]{2}](/latexrender/pictures/f9143e5f2d75ecc94f2b510b153fc539.png)
![cosx = - \frac{\sqrt[]{2}}{2} cosx = - \frac{\sqrt[]{2}}{2}](/latexrender/pictures/ad19c7ad5d6f6a25c027d3afb1a2ab87.png)
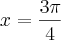

 , a equação
, a equação![\sqrt[]{1 - {sen}^{2}x} + cosx = - \sqrt[]{2} \sqrt[]{1 - {sen}^{2}x} + cosx = - \sqrt[]{2}](/latexrender/pictures/66cfc5cfae955058fcc408c85cf522ee.png)
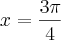
![\sqrt[]{{cos}^{2}x} + cosx = - \sqrt[]{2} \sqrt[]{{cos}^{2}x} + cosx = - \sqrt[]{2}](/latexrender/pictures/bda803f69f0e6db205a9a85df14f5f44.png)
![cosx + cosx = - \sqrt[]{2} cosx + cosx = - \sqrt[]{2}](/latexrender/pictures/f9143e5f2d75ecc94f2b510b153fc539.png)
![cosx = - \frac{\sqrt[]{2}}{2} cosx = - \frac{\sqrt[]{2}}{2}](/latexrender/pictures/ad19c7ad5d6f6a25c027d3afb1a2ab87.png)
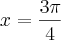

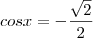 , você estaria certa, pois, de fato, no intervalo
, você estaria certa, pois, de fato, no intervalo  ,
,  deveria ser sim
deveria ser sim 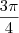 .
.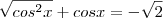

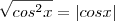
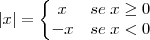
 , o sinal é indiferente, portanto, também pode ser assim:
, o sinal é indiferente, portanto, também pode ser assim: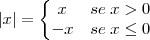
é que apenas um caso é considerado:
.
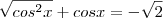

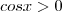
 .
.


 .
.



 .
.
 :
: