 por SsEstevesS » Dom Mar 18, 2012 21:30
por SsEstevesS » Dom Mar 18, 2012 21:30
Olá,
Vejamos se alguém sabe como resolver esta questão, estou precisando.....
Postei 2 fotos para entenderem melhor o desenho e o que se pede.
Eu ja fiz a letra A, mas nao conssigo fazer a B.
Na figura abaixo temos uma sucessao de triangulos retangulos em que um de seus catetos mede 1cm. Cada angulo TETAn, onde n=1,2,3,4..... , o n representa o angulo formado pela hipotenusa e um cateto de 1cm. Faça o que se pede:



- Anexos
-
- Foto2
-
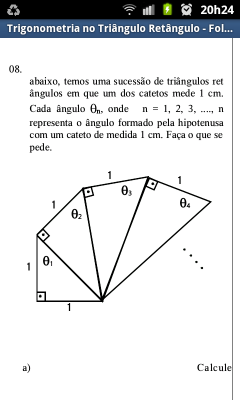
- Foto1
-
SsEstevesS
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Dom Nov 27, 2011 10:06
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: CEFET
- Andamento: cursando
 por MarceloFantini » Dom Mar 18, 2012 23:56
por MarceloFantini » Dom Mar 18, 2012 23:56
Mostre o seu raciocínio na letra a, pois dele a letra b segue.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por SsEstevesS » Seg Mar 19, 2012 00:21
por SsEstevesS » Seg Mar 19, 2012 00:21
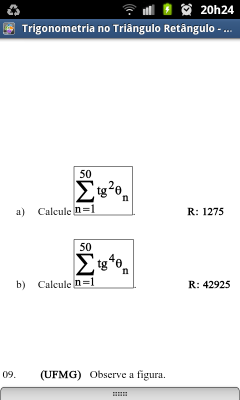
Fiz PA
amanha mostro o que fiz para chegar na PA
creio que a b, seja PA de 2 ordem....
Mas nao sei como calcular somatorio dos fatores de PA de 2 ordem!
-
SsEstevesS
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Dom Nov 27, 2011 10:06
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: CEFET
- Andamento: cursando
 por MarceloFantini » Seg Mar 19, 2012 00:38
por MarceloFantini » Seg Mar 19, 2012 00:38
Se por progressão aritmética de "segunda ordem" você diz

, está errado. Isto não é progressão aritmética, é apenas a soma de quadrados. Vai a dica:
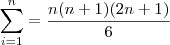
. Usando isso você deve chegar na resposta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por SsEstevesS » Seg Mar 19, 2012 14:28
por SsEstevesS » Seg Mar 19, 2012 14:28
Po cara,
é isso ai... Muito obrigado!
Mas voce sabe como se chega nesta formula? qualo caminho que se percorre para chegar la?
grato!
-
SsEstevesS
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Dom Nov 27, 2011 10:06
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: CEFET
- Andamento: cursando
 por MarceloFantini » Seg Mar 19, 2012 18:53
por MarceloFantini » Seg Mar 19, 2012 18:53
Não sei deduzir esta expressão, mas sei provar que ela é válida sempre, usando princípio da indução finita. Em todo caso, sabendo-a você já consegue resolver o problema.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Seg Mar 19, 2012 22:02
por LuizAquino » Seg Mar 19, 2012 22:02
MarceloFantini escreveu:Vai a dica:
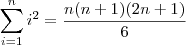
.
SsEstevesS escreveu:Mas voce sabe como se chega nesta formula? qualo caminho que se percorre para chegar la?
MarceloFantini escreveu:Não sei deduzir esta expressão, mas sei provar que ela é válida sempre, usando princípio da indução finita.
Vamos começar a justificativa desenvolvendo o seguinte somatório:
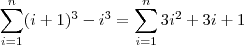
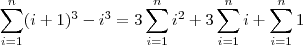
No segundo membro, note que o primeiro somatório é exatamente o que queremos obter. Já o segundo é uma p. a. de primeiro termo 1, razão 1 e último termo n. Por fim, no terceiro estamos somando o número 1 uma quantidade n de vezes. Desse modo, temos que:
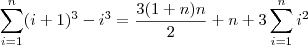
Por outro lado, temos que:
![\sum_{i=1}^n (i+1)^3 - i^3 = (\cancel{2^3} - 1^3) + (\cancel{3^3} - \cancel{2^3}) + (\cancel{4^3} - \cancel{3^3}) + \cancel{\cdots} + [(n+1)^3 - \cancel{n^3}] \sum_{i=1}^n (i+1)^3 - i^3 = (\cancel{2^3} - 1^3) + (\cancel{3^3} - \cancel{2^3}) + (\cancel{4^3} - \cancel{3^3}) + \cancel{\cdots} + [(n+1)^3 - \cancel{n^3}]](/latexrender/pictures/903da68a51eddbc3751a1cac8fae965c.png)
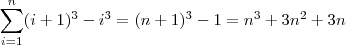
Usando as informações anteriores, temos que:
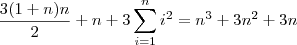
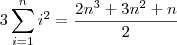
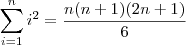
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Alguem sabe a Resolucao desta questao?
 por SsEstevesS » Sex Mar 16, 2012 16:07
por SsEstevesS » Sex Mar 16, 2012 16:07
- 6 Respostas
- 3937 Exibições
- Última mensagem por SsEstevesS

Sáb Mar 17, 2012 21:07
Geometria Espacial
-
- Por favor alguém sabe resolver esta questão
por costav13 » Sáb Nov 09, 2013 10:10
- 3 Respostas
- 2576 Exibições
- Última mensagem por e8group

Dom Nov 10, 2013 13:29
Cálculo: Limites, Derivadas e Integrais
-
- N entendi a resolucao, questao de g p, alguem pode explicar?
por bmachado » Ter Mar 27, 2012 00:32
- 1 Respostas
- 4037 Exibições
- Última mensagem por bmachado

Ter Mar 27, 2012 22:35
Geometria Plana
-
- Alguém sabe?
por Cleyson007 » Sex Jan 11, 2013 16:47
- 1 Respostas
- 2318 Exibições
- Última mensagem por Jhenrique

Sáb Jan 12, 2013 18:31
Pedidos de Materiais
-
- gostaria de ajuda na resoluçao desta integral
por nayyricarda » Sex Out 01, 2010 16:36
- 2 Respostas
- 3076 Exibições
- Última mensagem por Moura

Ter Dez 14, 2010 13:36
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







 , está errado. Isto não é progressão aritmética, é apenas a soma de quadrados. Vai a dica:
, está errado. Isto não é progressão aritmética, é apenas a soma de quadrados. Vai a dica: 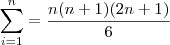 . Usando isso você deve chegar na resposta.
. Usando isso você deve chegar na resposta.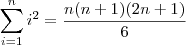 .
. 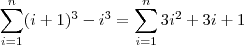
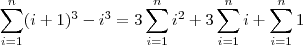
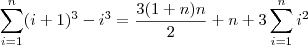
![\sum_{i=1}^n (i+1)^3 - i^3 = (\cancel{2^3} - 1^3) + (\cancel{3^3} - \cancel{2^3}) + (\cancel{4^3} - \cancel{3^3}) + \cancel{\cdots} + [(n+1)^3 - \cancel{n^3}] \sum_{i=1}^n (i+1)^3 - i^3 = (\cancel{2^3} - 1^3) + (\cancel{3^3} - \cancel{2^3}) + (\cancel{4^3} - \cancel{3^3}) + \cancel{\cdots} + [(n+1)^3 - \cancel{n^3}]](/latexrender/pictures/903da68a51eddbc3751a1cac8fae965c.png)
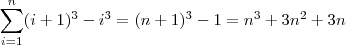
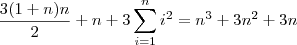
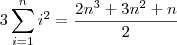
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
