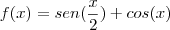por rodsales » Sáb Jun 06, 2009 21:09
por rodsales » Sáb Jun 06, 2009 21:09
Tenho duas dúvidas. A primeira, a função seno como função ímpar(explicar mais para leigo entender, não como nos livros de matemática). Eu não entendi por que é função ímpar.
Já a segunda, dê o período da função y=|sen x|. Para saber o período era só pegar o coeficiente de x e jogar na expressão
p=2
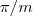
. Para mim como resposta seria 2

, pois o coeficiente é 1. Mas, a resposta do livro está como

.
Grato,
Aguardo Respostas.
-

rodsales
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Ter Abr 14, 2009 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por Marcampucio » Sáb Jun 06, 2009 21:44
por Marcampucio » Sáb Jun 06, 2009 21:44
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por rodsales » Dom Jun 07, 2009 15:24
por rodsales » Dom Jun 07, 2009 15:24
Então para a segunda pergunta, quando temos módulo o mais certo para sabermos o período é criar um gráfico, em vez de confiarmos naquela expressão?
Grato,
Aguardo Respostas.
-

rodsales
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Ter Abr 14, 2009 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por Marcampucio » Dom Jun 07, 2009 15:45
por Marcampucio » Dom Jun 07, 2009 15:45
Aquela regra é boa para a função
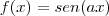
, pois se baseia no fato de que o período fundamental de

é
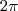
.
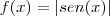
é
outra função cujo período fundamental é

. Podemos analogamente dizer que o período de
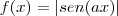
é

é sempre importante conhecer a função com alguma intimidade. Encontrar períodos não é tão simples como parece à primeira vista. Veja o caso do período de
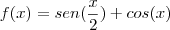

A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda sobre Limites seno e exponencial
por gn66 » Sex Jun 03, 2011 12:02
- 8 Respostas
- 5078 Exibições
- Última mensagem por gn66

Sex Jun 03, 2011 16:34
Cálculo: Limites, Derivadas e Integrais
-
- Duvida em seno e coSSeno(editada)
 por bmachado » Sex Jun 01, 2012 00:20
por bmachado » Sex Jun 01, 2012 00:20
- 1 Respostas
- 1283 Exibições
- Última mensagem por Russman

Sex Jun 01, 2012 02:03
Trigonometria
-
- Dúvida em valores de seno, cosseno e tangente.
 por Sobreira » Ter Abr 30, 2013 00:40
por Sobreira » Ter Abr 30, 2013 00:40
- 1 Respostas
- 1385 Exibições
- Última mensagem por young_jedi

Ter Abr 30, 2013 12:52
Trigonometria
-
- dúvida, derivar seno e cosseno até a terceira ordem
por PORTER » Qui Dez 11, 2014 08:10
- 1 Respostas
- 1342 Exibições
- Última mensagem por adauto martins

Sex Dez 12, 2014 11:34
Cálculo: Limites, Derivadas e Integrais
-
- [derivadas] - dúvida: função quociente entre seno e arcotang
por EnGENheiro_nota10 » Qui Set 26, 2013 21:22
- 3 Respostas
- 2307 Exibições
- Última mensagem por EnGENheiro_nota10

Dom Nov 03, 2013 11:17
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
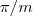 . Para mim como resposta seria 2
. Para mim como resposta seria 2 , pois o coeficiente é 1. Mas, a resposta do livro está como
, pois o coeficiente é 1. Mas, a resposta do livro está como  .
.
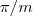 . Para mim como resposta seria 2
. Para mim como resposta seria 2 , pois o coeficiente é 1. Mas, a resposta do livro está como
, pois o coeficiente é 1. Mas, a resposta do livro está como  .
.





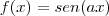 , pois se baseia no fato de que o período fundamental de
, pois se baseia no fato de que o período fundamental de  é
é 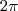 .
. 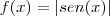 é outra função cujo período fundamental é
é outra função cujo período fundamental é  . Podemos analogamente dizer que o período de
. Podemos analogamente dizer que o período de 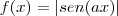 é
é