 por andersontricordiano » Qua Jan 18, 2012 21:44
por andersontricordiano » Qua Jan 18, 2012 21:44
a) Calcule

,

e

, sabendo que

b)Suponha o caso particular em que a=0 e , fazendo as adaptações necessárias na resposta do item (a) verifique a coerência de tal resposta.
Respostas:
a)
![sen\theta=+-\frac{a\sqrt[]{{a}^{2}+{b}^{2}}}{{a}^{2}+{b}^{2}} sen\theta=+-\frac{a\sqrt[]{{a}^{2}+{b}^{2}}}{{a}^{2}+{b}^{2}}](/latexrender/pictures/edbf30afddea84511531ab08380883f3.png)
![sen\theta=+-\frac{b\sqrt[]{{a}^{2}+{b}^{2}}}{{a}^{2}+{b}^{2}} sen\theta=+-\frac{b\sqrt[]{{a}^{2}+{b}^{2}}}{{a}^{2}+{b}^{2}}](/latexrender/pictures/7a56452b49f43e721195b58892b65bb3.png)
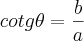
b)

-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por ant_dii » Qui Jan 19, 2012 01:55
por ant_dii » Qui Jan 19, 2012 01:55
Na verdade temos

E como

, temos

.
Como
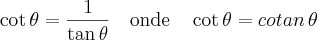
, então
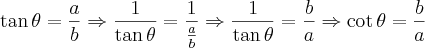
.
Quanto a questão b), teremos


Mas para o caso de que

, tem-se que usar outro recurso, o limite de uma função pois

não pode ser zero...
Logo, suas respostas estavam todas corretas e só não entendi qual era a dúvida então...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivadas com cotg e cos sen e cos
por Matheus321 » Seg Nov 21, 2016 16:47
- 1 Respostas
- 5082 Exibições
- Última mensagem por Cleyson007

Seg Nov 21, 2016 20:46
Cálculo: Limites, Derivadas e Integrais
-
- Geometria - sen?, tg?, cotg?, cos?, sec?, cossec?
 por jp_jp300 » Ter Set 25, 2007 18:57
por jp_jp300 » Ter Set 25, 2007 18:57
- 6 Respostas
- 10363 Exibições
- Última mensagem por admin

Ter Mar 11, 2008 21:28
Trigonometria
-
- P.G., calcule Sn=9+99+999... +10n-1
por georgefdfdl » Qui Nov 10, 2011 23:49
- 1 Respostas
- 1620 Exibições
- Última mensagem por LuizAquino

Sex Nov 11, 2011 17:41
Progressões
-
- calcule y
por Guilhermme » Sáb Mar 31, 2012 17:06
- 4 Respostas
- 4060 Exibições
- Última mensagem por Nico Romani

Qui Mar 31, 2016 17:01
Geometria Analítica
-
- Calcule a e b
por andersontricordiano » Dom Mar 02, 2014 12:01
- 3 Respostas
- 4659 Exibições
- Última mensagem por nat-larissa

Seg Mar 03, 2014 20:12
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ,
,  e
e  , sabendo que
, sabendo que 
![sen\theta=+-\frac{a\sqrt[]{{a}^{2}+{b}^{2}}}{{a}^{2}+{b}^{2}} sen\theta=+-\frac{a\sqrt[]{{a}^{2}+{b}^{2}}}{{a}^{2}+{b}^{2}}](/latexrender/pictures/edbf30afddea84511531ab08380883f3.png)
![sen\theta=+-\frac{b\sqrt[]{{a}^{2}+{b}^{2}}}{{a}^{2}+{b}^{2}} sen\theta=+-\frac{b\sqrt[]{{a}^{2}+{b}^{2}}}{{a}^{2}+{b}^{2}}](/latexrender/pictures/7a56452b49f43e721195b58892b65bb3.png)
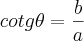


 ,
,  e
e  , sabendo que
, sabendo que 
![sen\theta=+-\frac{a\sqrt[]{{a}^{2}+{b}^{2}}}{{a}^{2}+{b}^{2}} sen\theta=+-\frac{a\sqrt[]{{a}^{2}+{b}^{2}}}{{a}^{2}+{b}^{2}}](/latexrender/pictures/edbf30afddea84511531ab08380883f3.png)
![sen\theta=+-\frac{b\sqrt[]{{a}^{2}+{b}^{2}}}{{a}^{2}+{b}^{2}} sen\theta=+-\frac{b\sqrt[]{{a}^{2}+{b}^{2}}}{{a}^{2}+{b}^{2}}](/latexrender/pictures/7a56452b49f43e721195b58892b65bb3.png)
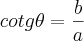



 , temos
, temos .
.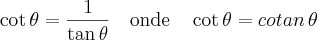 , então
, então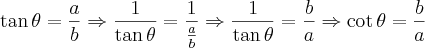 .
.

 , tem-se que usar outro recurso, o limite de uma função pois
, tem-se que usar outro recurso, o limite de uma função pois  não pode ser zero...
não pode ser zero...