Quantas soluções a equação trigonométrica sen^6(x) + cos^6(x) = 1 admite no intervalo [0, 100]?
A) 64
B) 60
C) 56
D) 52
E) 48
Questão 21 da prova da Uespi 2011.



![(senx)^6 + [(cosx)^2]^3 = 1 (senx)^6 + [(cosx)^2]^3 = 1](/latexrender/pictures/f511cc129fdc4359e16eb6026ce85ddd.png)
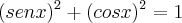
 e substituindo na equação original, teremos:
e substituindo na equação original, teremos:![(senx)^6 + [1-(senx)^2]^3 = 1 (senx)^6 + [1-(senx)^2]^3 = 1](/latexrender/pictures/837fd4963d0ddb0ebf1a95e8eafda613.png)
![(senx)^6 + 1 + 3*1*[(senx)^2]^2 - 3*1^2*(senx)^2 - (senx)^6 = 1 (senx)^6 + 1 + 3*1*[(senx)^2]^2 - 3*1^2*(senx)^2 - (senx)^6 = 1](/latexrender/pictures/96aaeaaa1b582519db3d83914875119d.png)


![(senx)^2*[ (senx)^2 - 1 ]= 0 (senx)^2*[ (senx)^2 - 1 ]= 0](/latexrender/pictures/0c38213f9da2c2e377facb6d74014742.png)
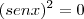 ou
ou 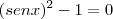

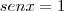
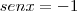
![x \in [ 0 ; 100 ] x \in [ 0 ; 100 ]](/latexrender/pictures/1f1152c6929984e78fdc3eabe4a27eb7.png)
 rad
rad  6,18 rad
6,18 rad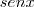 :
:
 implica em dois pontos : 0 e 2
implica em dois pontos : 0 e 2
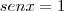
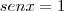 implica em apenas um ponto :
implica em apenas um ponto : 
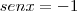
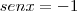 implica em apenas um ponto :
implica em apenas um ponto :

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.