por andersontricordiano » Ter Out 04, 2011 15:32
Na circunferência de raio r e centro O, abaixo, considera-se um arco AP, no sentido anti-horario, que mede 2 radianos. A respeito do ponto P, pode-se afirmar que:
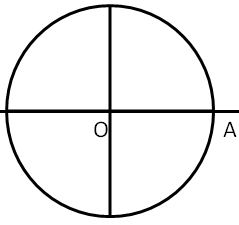
- circulo22222.gif (3.24 KiB) Exibido 1497 vezes
Resposta é 2º quadrante
Gostaria de saber porque é no 2º quadrante pois nos meus calculo entendo que é na mesma posição de A já que um radiano é iqual a 180º.. Agradeço quem me explicar !
-
andersontricordiano
- Colaborador Voluntário
-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
por joaofonseca » Ter Out 04, 2011 16:57
Estás a confundir 1 radiano com
radianos.
Observa está figura.
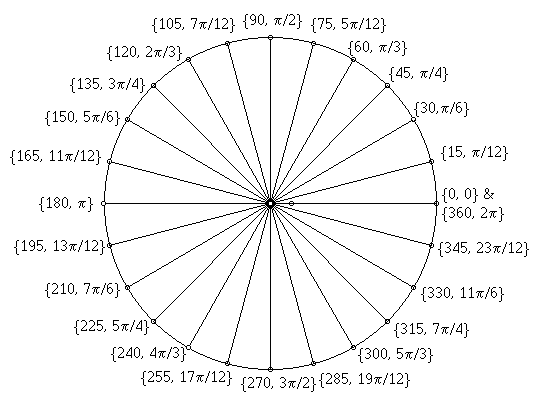
- circle_degrad.gif (9.21 KiB) Exibido 1490 vezes
-
joaofonseca
- Colaborador Voluntário
-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ponto da reta r que é eqüidistante do ponto A e do ponto B
por gutorocher » Qua Jul 21, 2010 14:01
- 12 Respostas
- 15247 Exibições
- Última mensagem por gutorocher
Sex Jul 23, 2010 13:04
Geometria Analítica
-
- [Vetores] Ponto de reta próximo a outros pares de ponto
por cmcrz97 » Ter Jun 19, 2018 20:29
- 0 Respostas
- 3031 Exibições
- Última mensagem por cmcrz97
Ter Jun 19, 2018 20:29
Álgebra Linear
-
- [Ponto Crítico e Ponto de Inflexão e intervalos] Dúvidas em
por Andre Lopes » Qua Set 26, 2012 00:37
- 2 Respostas
- 3403 Exibições
- Última mensagem por MarceloFantini
Qui Set 27, 2012 06:56
Cálculo: Limites, Derivadas e Integrais
-
- quadrante
por leticiapires52 » Sex Ago 29, 2014 13:50
- 2 Respostas
- 2489 Exibições
- Última mensagem por jcmatematica
Dom Ago 31, 2014 12:50
Trigonometria
-
- Redução de quadrante
por Edla Matias » Dom Dez 18, 2011 12:59
- 0 Respostas
- 902 Exibições
- Última mensagem por Edla Matias
Dom Dez 18, 2011 12:59
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 15 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
