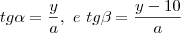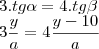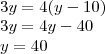por Guilherme Carvalho » Sex Mai 13, 2011 14:08
por Guilherme Carvalho » Sex Mai 13, 2011 14:08
Dois edificios
X e
Y, estão um em frete ao outro, num terreno plano. Um observador, no pé do edifício
X(Ponto
P), mede um angulo
? em relação ao topo do edifício
Y(Ponto
Q). Depois disso, no topo do edifício
X, num ponto
R, de forma que RPTS formem um retângulo e QT seja perpendicular a PT, esse observador mede um ângulo
ß em relação ao ponto
Q no edifício
Y.

Sabendo que a altura do edifício
X é 10m e que 3.tg? = 4.tgß, a altura
h do edifício
Y, em metros é
a)40/3
b)50/4
c)30
d)40
e)50
-
Guilherme Carvalho
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Mar 03, 2011 12:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecatrônica
- Andamento: cursando
 por carlosalesouza » Sex Mai 13, 2011 17:04
por carlosalesouza » Sex Mai 13, 2011 17:04
vamos chamar a distância entre os prédios(PT) de a, ok?
sendo
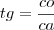
, então:
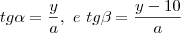
Então, usando a relação conhecida entre as tangentes:
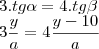
Como ambos os lados estão sendo divididos por a, se multiplicarmos ambos por a, ele será anulado e teremos:
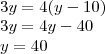
Temos nossa resposta... rs
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Triangulos] Questão Unesp-93
por Ludmilla_Mayer » Seg Mar 10, 2014 22:31
- 3 Respostas
- 5542 Exibições
- Última mensagem por Ludmilla_Mayer

Seg Mar 17, 2014 12:20
Geometria Plana
-
- Questão Unesp - Pirâmide (Ajudem!)
 por kamillanjb » Qua Jun 29, 2011 19:45
por kamillanjb » Qua Jun 29, 2011 19:45
- 2 Respostas
- 3061 Exibições
- Última mensagem por kamillanjb

Sex Jul 22, 2011 15:02
Geometria Espacial
-
- (Unesp) sistema linear questão 36
por lnd_rj1 » Dom Fev 10, 2013 09:09
- 0 Respostas
- 1512 Exibições
- Última mensagem por lnd_rj1

Dom Fev 10, 2013 09:09
Álgebra Linear
-
- função - unesp
por karen » Ter Nov 27, 2012 20:01
- 4 Respostas
- 6010 Exibições
- Última mensagem por karen

Ter Nov 27, 2012 20:47
Funções
-
- Unesp - 95 Números Complexos
por Alucard014 » Dom Ago 01, 2010 18:22
- 1 Respostas
- 51753 Exibições
- Última mensagem por MarceloFantini

Qui Ago 05, 2010 17:27
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




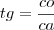 , então:
, então: