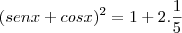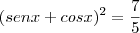por wallsoares » Qua Mar 23, 2011 01:25
por wallsoares » Qua Mar 23, 2011 01:25
Pessoal, precisa de uma ajuda no seguinte exercicio:
se
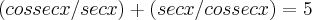
então quanto é
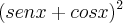
Olhem até onde eu fui:~
como
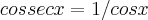
e
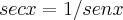
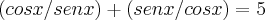
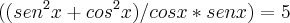
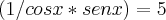
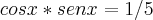
Empaquei aí, será que alguém poderia me ajudar no próximo passo ou verificar se estou indo pelo caminho correto?
Muito obrigado
-
wallsoares
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Mar 21, 2011 19:48
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Qua Mar 23, 2011 11:06
por LuizAquino » Qua Mar 23, 2011 11:06
wallsoares escreveu:cossec x = 1/cosx e sec x = 1/senx
Correção:
(i)
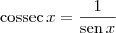
(ii)
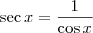
Desse modo, temos que:
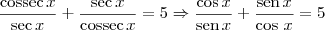
Agora tente desenvolver o resto lembrando-se do produto notável:
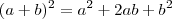
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por wallsoares » Qui Mar 24, 2011 00:15
por wallsoares » Qui Mar 24, 2011 00:15
Obrigado pela correção, professor.
Porém não consegui desenvolver muito, mesmo com sua dica sobre o produto notável:
Parei novamente na seguinte posição:

Poderia me dar mais uma dica do próximo passo?
Muito obrigado
-
wallsoares
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Mar 21, 2011 19:48
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por FilipeCaceres » Qui Mar 24, 2011 00:39
por FilipeCaceres » Qui Mar 24, 2011 00:39
Continuando a questão...
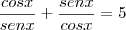
Logo,
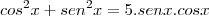
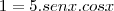
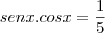
(i)
Agora vamos para o que se pede:
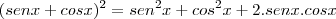

(ii)
De (i) em (ii) temos
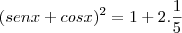
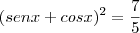
Espero ter ajudado.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por wallsoares » Qui Mar 24, 2011 01:26
por wallsoares » Qui Mar 24, 2011 01:26
Prezado Felipe,
Muito obrigado pelo esclarecimento.
Forte abraço.
-
wallsoares
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Mar 21, 2011 19:48
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [ajuda]trigonometria
por victorrocha31 » Dom Nov 22, 2009 20:57
- 2 Respostas
- 3374 Exibições
- Última mensagem por victorrocha31

Seg Nov 23, 2009 00:34
Trigonometria
-
- Trigonometria Ajuda!
por JustForFun » Sex Nov 05, 2010 22:42
- 7 Respostas
- 4516 Exibições
- Última mensagem por JustForFun

Dom Nov 07, 2010 01:22
Trigonometria
-
- ajuda em trigonometria
 por buzinaaroo » Qua Nov 10, 2010 10:05
por buzinaaroo » Qua Nov 10, 2010 10:05
- 3 Respostas
- 2390 Exibições
- Última mensagem por Jefferson

Qui Nov 18, 2010 15:44
Trigonometria
-
- Ajuda com trigonometria 9º ano
por AndreiOEstudioso » Sáb Abr 23, 2011 13:24
- 2 Respostas
- 2452 Exibições
- Última mensagem por AndreiOEstudioso

Dom Abr 24, 2011 11:21
Trigonometria
-
- ajuda trigonometria 11º ano
por tiagofe » Ter Abr 26, 2011 19:59
- 5 Respostas
- 3519 Exibições
- Última mensagem por tiagofe

Qua Abr 27, 2011 12:52
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
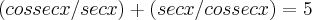
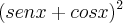
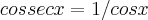 e
e 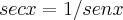
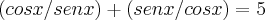
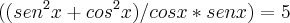
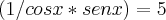
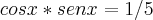

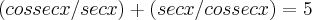
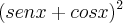
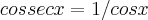 e
e 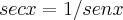
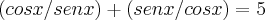
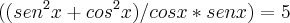
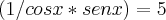
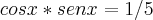

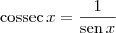
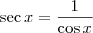
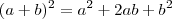 .
.


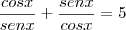
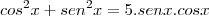
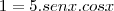
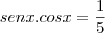 (i)
(i)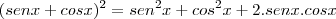
 (ii)
(ii)