 por vinicius cruz » Qui Mar 17, 2011 15:09
por vinicius cruz » Qui Mar 17, 2011 15:09
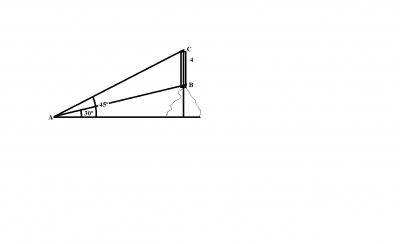
de um ponto A no solo, visa-se a base B e o topo C de um bastão colocado verticalmente no alto de uma colina, sob os angulos 30º e 45º, respectivamente. Se o bastão mede 4 metros de comprimento, a altura da colina é:
olha a imagem
http://img21.imageshack.us/i/semttulofeq.png/a)?3
b)2?2
c)2(?3+1)
d)2(?3+3)
e)2+?3
- Anexos
-
-
vinicius cruz
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Mar 06, 2011 12:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por Elcioschin » Qui Mar 17, 2011 18:34
por Elcioschin » Qui Mar 17, 2011 18:34
Seja h altura da colina e d a distância horizontal
tg30º = h/d ----> 1/V3 = h/d ----> d = V3*h ----> I
tg45º = (h + 4)/d ----> 1 = (h + 4)/d ----> d = h + 4 ----> II
I = II ----> V3*h = h + 4 ----> V3*h - h = 4 ----> (V3 - 1)*h = 4 ----> h = 4/(V3 - 1) ----> Racionalizando:
h = 4*(V3 + 1)/(V3 - 1)*(V3 + 1) ----> h = 4*(V3 + 1)/(3 - 1) ----> h = 2*(V3 + 1) ----> Alternativa C
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- trigonometria- matemática
 por zenildo » Sáb Abr 06, 2013 21:22
por zenildo » Sáb Abr 06, 2013 21:22
- 1 Respostas
- 2916 Exibições
- Última mensagem por DanielFerreira

Dom Abr 07, 2013 12:03
Trigonometria
-
- trigonometria- matemática
por zenildo » Qui Abr 11, 2013 16:08
- 1 Respostas
- 913 Exibições
- Última mensagem por e8group

Qui Abr 11, 2013 17:57
Trigonometria
-
- [trigonometria] trigonometria em triangulo qualquer
por biamassa00 » Sex Mai 25, 2012 22:19
- 0 Respostas
- 3591 Exibições
- Última mensagem por biamassa00

Sex Mai 25, 2012 22:19
Trigonometria
-
- (Trigonometria) problema trigonometria
por Luizap11 » Qui Dez 05, 2013 00:33
- 2 Respostas
- 5268 Exibições
- Última mensagem por Edunclec

Qui Dez 05, 2013 20:53
Trigonometria
-
- Matemática Financeira: matemática
por Victor Gabriel » Sex Mai 10, 2013 02:49
- 1 Respostas
- 3143 Exibições
- Última mensagem por killua05

Qua Mai 29, 2013 13:49
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 .
.
 :
: