exercícios de triangulos retangulos

[analuiza]

to com uma lista de exercícios,e preciso fazer 10 questões até segunda se não o professor vai me suspender.se puderem me ajudem
1)As razões trigonométricas seno,cosseno,tangente.são razões entre os lados de um triangulo retângulo.na construção abaixo,podemos escrever que:
tg = ===.
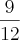Nessas condições,então sen + cos vale:
a)1 b) c) d) e)


2)Uma cidade planejada foi construída com seu sistema de esgoto obedecendo á esquematização de uma malha línear representada no gráfico a seguir,onde cada vésrtice dista do adjacente uma unidade.Os pontos A e B representam duas casas e o ponto O,a origem de uma confluêmcoa de canos que necessitam de uma' luva de união '.o valor do seno do angulo que leva a união em O possui é :
a)1/2 b)raiz de 2 sobre 2 c)raiz de 3 sobre 3 d)4 raiz de 17 sobre 17 e) 2 raiz de 17 sobre 17

3)a figura abaixo mostra uma piscina em formato retangular ABCD .Se a largura (AB)da piscina mede 15 m e o ângulo formado pela trajetoria do nadador com a borda (AB) da piscina é 60ºma distancia de (d) pecorrida por uma pessoa que deseja nadar do ponto A até o ponto C em linha reta é :
a)7.5m b)7,5 raiz de 3 m c)15 raiz de 3 m d)30 m e)30 raiz de 3 m

4)Considere uma torre,um observador situado a 300 metros dela e o ângulo de 11° que é formado entre o observador e o ponto mais alto da torre.A altura dessa torre é :
a) 30 m b)45 m c)58 m d)62m e)71 m

5)Um avião decola,pecorrendo uma trajetória retilínea,fprmando com o solo um ângulo de 30°(suponha que a região sobrevoada pelo avião seja plana).Depois de pecorrer 1.000 metros,a altura atingida pelo avião em metros é:
a)500 b)750 c)1.000 d)1250 e)1500

6)Ao aproximar-se se uma ilha o capitão de um navio avistou uma motanha e decidiu medir sua altura .Ele mediu um ângulo de 30° na direção do cume.Depois de navegar mais 2 km em direção á montanha,repitiu o procedimento medindo novo ângulo de 45º.então usando raiz de 3 = 1,73,o valor mais proximo da aultura dessa montanha em quilômetros é :
a)2,1 b)2.2 c)2,5 d)2,7 e)3,0

7) Se um cateto e a hipotenusa de um triangulo retangulo medem 2a e 4a,respectivamente entao a tangente do angulo oposto ao menos lado é :
a)2 raiz de 3 b)raiz de 3 sobre 3 c)raiz de 3 sobre 6 d )raiz de vinte sobre vinte e)3 raiz de 3

8)Uma escada que mede 6m está apoiada em uma parede.Sabendo-se que ela forma com o solo um angulo e que cos=raiz de 5 sobre 3,a distancia de seu ponto de apoio na parede até o solo em metros é :a)4 b)5 c)2 raiz de 5 d)3 raiz de 5 e)raiz de 10


gente por favor me ajudem..

[DanielRJ]

o Objetivo do forum não é resolver lista de exercicios poste somente uma questão por topico e expresse sua duvida. Para podemos sana-lás.